题目内容
2. 如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B
如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B(1)求证:直线CD是⊙O的切线;
(2)如果D点是BC的中点,⊙O的半径为3cm,求$\widehat{DE}$的长度(结果保留π)
分析 (1)欲证明直线CD是⊙O的切线,只要证明∠ODC=90°即可.
(2)先证明∠B=∠OCB=∠ACO,推出∠B=30°,∠DOE=60°,利用弧长公式即可解决问题.
解答 (1) 证明:∵AC是⊙O切线,
证明:∵AC是⊙O切线,
∴OA⊥AC,
∴∠OAC=90°,
∵CO平分∠AOD,
∴∠AOC=∠COD,
在△AOC和△DOC中,
$\left\{\begin{array}{l}{OC=OC}\\{∠COA=∠COD}\\{OA=OD}\end{array}\right.$,
∴△AOC≌△DOC,
∴∠ODC=∠OAC=90°,
∴OD⊥CD,
∴直线CD是⊙O的切线.
(2)∵OD⊥BC,DC=DB,
∴OC=OB,
∴∠OCD=∠B=∠ACO,
∵∠B+∠ACB=90°,
∴∠B=30°,∠DOE=60°,
∴$\widehat{DE}$的长=$\frac{60π•3}{180}$=π.
点评 本题考查切线的判定和性质、弧长公式、线段的垂直平分线的性质、全等三角形的判定和性质等知识,属于中考常考题型;解题的关键是发现全等三角形,证明∠B=30°.

练习册系列答案
相关题目
12.小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15分钟的频率是( )
| 通话时间x/分钟 | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 16 | 9 | 5 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.9 |
17.某校九年级(1)班全体学生上周末进行体育测试的成绩(满分70分)统计如表:
根据表中的信息判断,下列结论中错误的是( )
| 成绩(分) | 45 | 50 | 55 | 60 | 65 | 68 | 70 |
| 人数(人) | 2 | 6 | 10 | 7 | 6 | 5 | 4 |
| A. | 该班一共有40名同学 | |
| B. | 该班学生这次测试成绩的众数是55分 | |
| C. | 该班学生这次测试成绩的中位数是60分 | |
| D. | 该班学生这次测试成绩的平均数是59分 |
7.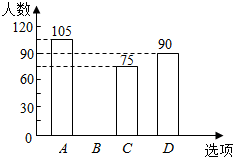 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
请结合统计图表,回答下列问题:
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
 某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:
某校在民族团结宣传活动中,采用了四种宣传形式:A唱歌,B舞蹈,C朗诵,D器乐.全校的每名学生都选择了一种宣传形式参与了活动,小明对同学们选用的宣传形式,进行了随机抽样调查,根据调查统计结果,绘制了如图两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 唱歌 | 35% |
| B | 舞蹈 | a |
| C | 朗诵 | 25% |
| D | 器乐 | 30% |
(1)本次调查的学生共300人,a=10%,并将条形统计图补充完整;
(2)如果该校学生有2000人,请你估计该校喜欢“唱歌”这种宣传形式的学生约有多少人?
(3)学校采用调查方式让每班在A、B、C、D四种宣传形式中,随机抽取两种进行展示,请用树状图或列表法,求某班抽到的两种形式恰好是“唱歌”和“舞蹈”的概率.
11.计算正确的是( )
| A. | (-5)0=0 | B. | x2+x3=x5 | C. | (ab2)3=a2b5 | D. | 2a2•a-1=2a |
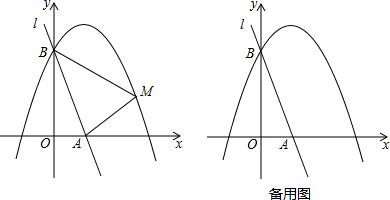
 已知二次函数y=x2-(2k+1)x+k2+k(k>0)
已知二次函数y=x2-(2k+1)x+k2+k(k>0)