题目内容
13.有一箱子装有3张分别标示1、5、8的号码牌,已知小明以每次取一张且取后不放回的方式,先后取出2张牌,组成一个两位数,取出第1张牌的号码为十位数,第2张牌的号码为个位数,则组成的二位数能被3整除的概率是$\frac{2}{3}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与组成的二位数能被3整除的情况,再利用概率公式求解即可求得答案.
解答 解:画树状图得:
∵共有6种等可能的结果,组成的二位数能被3整除的有4种情况,
∴组成的二位数能被3整除的概率是:$\frac{4}{6}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
3. 已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.
已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.
 已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.
已知:如图,在矩形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点F从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点F的运动时间为y秒,当y的值为( )秒时,△ABF和△DCE全等.| A. | 1 | B. | 1或3 | C. | 1或7 | D. | 3或7 |
8.不等式组$\left\{\begin{array}{l}{x+1>0}\\{-2x+4<0}\end{array}\right.$的解集是( )
| A. | x>-1 | B. | x<2 | C. | x>2 | D. | -1<x<2 |
18.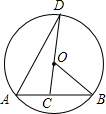 如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )
如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )
 如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )
如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )| A. | 30° | B. | 45° | C. | 20° | D. | 35° |
3.计算$\sqrt{3}$-$\sqrt{2}$的结果精确到0.01是(可用科学计算器计算或笔算)( )
| A. | 0.30 | B. | 0.31 | C. | 0.32 | D. | 0.33 |
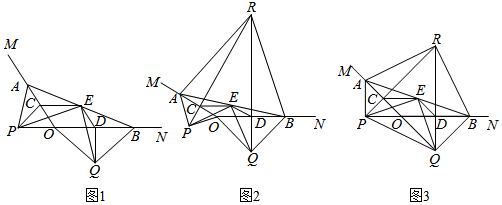
 如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B
如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B