题目内容
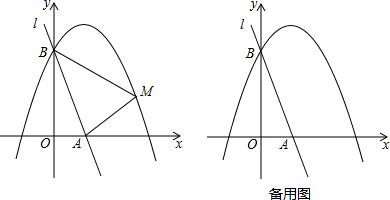
10.如图,直线l:y=-3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2-2ax+a+4(a<0)经过点B.(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
分析 (1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值;
(2)设M的坐标为(m,-m2+2m+3),然后根据面积关系将△ABM的面积进行转化;
(3)①由(2)可知m=$\frac{5}{2}$,代入二次函数解析式即可求出纵坐标的值;
②可将求d1+d2最大值转化为求AC的最小值.
解答 解:(1)令x=0代入y=-3x+3,
∴y=3,
∴B(0,3),
把B(0,3)代入y=ax2-2ax+a+4,
∴3=a+4,
∴a=-1,
∴二次函数解析式为:y=-x2+2x+3;
(2)令y=0代入y=-x2+2x+3,
∴0=-x2+2x+3,
∴x=-1或3,
∴抛物线与x轴的交点横坐标为-1和3,
∵M在抛物线上,且在第一象限内,
∴0<m<3,
令y=0代入y=-3x+3,
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,-m2+2m+3),
S=S四边形OAMB-S△AOB
=S△OBM+S△OAM-S△AOB
=$\frac{1}{2}$×m×3+$\frac{1}{2}$×1×(-m2+2m+3)-$\frac{1}{2}$×1×3
=-$\frac{1}{2}$(m-$\frac{5}{2}$)2+$\frac{25}{8}$
∴当m=$\frac{5}{2}$时,S取得最大值$\frac{25}{8}$.
(3)①由(2)可知:M′的坐标为($\frac{5}{2}$,$\frac{7}{4}$);
②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,
根据题意知:d1+d2=BF,
此时只要求出BF的最大值即可,
∵∠BFM′=90°,
∴点F在以BM′为直径的圆上,
设直线AM′与该圆相交于点H,
∵点C在线段BM′上,
∴F在优弧$\widehat{BM′H}$上,
∴当F与M′重合时,
BF可取得最大值,
此时BM′⊥l1,
∵A(1,0),B(0,3),M′($\frac{5}{2}$,$\frac{7}{4}$),
∴由勾股定理可求得:AB=$\sqrt{10}$,M′B=$\frac{5\sqrt{5}}{4}$,M′A=$\frac{\sqrt{85}}{4}$,
过点M′作M′G⊥AB于点G,
设BG=x,
∴由勾股定理可得:M′B2-BG2=M′A2-AG2,
∴$\frac{85}{16}$-($\sqrt{10}$-x)2=$\frac{125}{16}$-x2,
∴x=$\frac{5\sqrt{10}}{8}$,
cos∠M′BG=$\frac{BG}{M′B}$=$\frac{\sqrt{2}}{2}$,
∵l1∥l′,
∴∠BCA=90°,
∠BAC=45°
方法二:过B点作BD垂直于l′于D点,过M′点作M′E垂直于l′于E点,则BD=d1,ME=d2,
∵S△ABM′=$\frac{1}{2}$×AC×(d1+d2)
当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM′时取得最小值.
根据B(0,3)和M′($\frac{5}{2}$,$\frac{7}{4}$)可得BM′=$\frac{5\sqrt{5}}{4}$,
∵S△ABM=$\frac{1}{2}$×AC×BM′=$\frac{25}{8}$,∴AC=$\sqrt{5}$,
当AC⊥BM′时,cos∠BAC=$\frac{AC}{AB}$=$\frac{\sqrt{5}}{\sqrt{10}}$=$\frac{\sqrt{2}}{2}$,
∴∠BAC=45°.
点评 本题考查二次函数的综合问题,涉及待定系数求二次函数解析式,求三角形面积,圆的相关性质等知识,内容较为综合,学生需要认真分析题目,化动为静去解决问题.

 应用题作业本系列答案
应用题作业本系列答案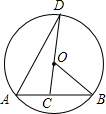 如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )
如图,己知AB、AD是⊙O的弦,∠B=20°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=15°,则∠BAD的度数是( )| A. | 30° | B. | 45° | C. | 20° | D. | 35° |
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
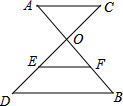 如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为$\frac{8}{3}$.
如图,AB、CD相交于点O,OC=2,OD=3,AC∥BD,EF是△ODB的中位线,且EF=2,则AC的长为$\frac{8}{3}$. 如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B
如图,OA,OD是⊙O半径,过A作⊙O的切线,交∠AOD的平分线于点C,连接CD,延长AO交⊙O于点E,交CD的延长线于点B