题目内容
12.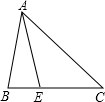 如图,在△ABC中,AB=AE,点E在AC的垂直平分线上.
如图,在△ABC中,AB=AE,点E在AC的垂直平分线上.(1)如果∠BAE=40°,那么∠B=70°,∠C=35°;
(2)已知△ABC的周长为20cm,AC=7cm,请你求出△ABE的周长.
分析 (1)根据等边对等角可得∠B=∠AEB,再利用三角形内角和定理可得∠B=∠AEB=$\frac{180°-40°}{2}$=70°,根据线段垂直平分线的性质可得AE=EC,再利用三角形外角的性质可得∠C的度数.
(2)根据题意可得AB+BC=13cm,利用等量代换可得AE+BE=BC,进而可得△ABE的周长.
解答 解:(1)∵AB=AE,
∴∠B=∠AEB,
∵∠BAE=40°,
∴∠B=∠AEB=$\frac{180°-40°}{2}$=70°,
∵点E在AC的垂直平分线上,
∴AE=EC,
∴∠C=∠EAC,
∴∠C=70°×$\frac{1}{2}$=35°,
故答案为:70;35.
(2)∵△ABC的周长为20cm,AC=7cm,
∴AB+BC=20-7=13(cm),
∵AE=EC,
∴AE+BE=BC,
∴△ABE的周长为:AB+BE+AE=AB+BC=13cm.
点评 此题主要考查了线段垂直平分线的性质,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 如图,在△ABC中,∠C=90°,∠A=30°,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC.求∠EDC的度数.
如图,在△ABC中,∠C=90°,∠A=30°,D、E分别为AC、AB上的点,且AD=BD,AE=BC,DE=DC.求∠EDC的度数. 如图,将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,连结AD,DC,∠DAB=30°,求证:AD2+AB2=AC2.
如图,将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,连结AD,DC,∠DAB=30°,求证:AD2+AB2=AC2.