题目内容
9. 如图,将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,连结AD,DC,∠DAB=30°,求证:AD2+AB2=AC2.
如图,将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,连结AD,DC,∠DAB=30°,求证:AD2+AB2=AC2.
分析 首先连接EA,将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,易得AC=DE,AB=BE,又由∠DAC=30°,继而可得∠DAE=90°,则可证得AD2+AB2=AC2.
解答  证明:连接AE,
证明:连接AE,
∵将△ABC绕顶点B按逆时针方向旋转60°,得到△EBD,
∵△ABC≌△EBD,
∴AC=DE,AB=BE,
∵∠ABE=60°,
∴BA=BE,∠BAE=60°,
∵∠DAB=30°,
∴∠DAE=90°,
∴DA2+EA2=DE2,
∴AD2+AB2=AC2.
点评 此题考查了旋转的性质以及勾股定理.此题难度适中,注意掌握旋转前后图形的对应关系,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
5.一元二次方程x2+2x+2=0根的情况是( )
| A. | 没有实数根 | B. | 有两个不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 不能确定 |

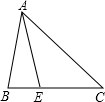 如图,在△ABC中,AB=AE,点E在AC的垂直平分线上.
如图,在△ABC中,AB=AE,点E在AC的垂直平分线上.
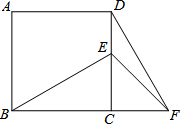 如图,在正方形ABCD中,E为CD边上的一点,F为BC延长线上一点,CE=CF,∠FDC=30°,则∠BEF的度数为105°.
如图,在正方形ABCD中,E为CD边上的一点,F为BC延长线上一点,CE=CF,∠FDC=30°,则∠BEF的度数为105°.