题目内容
16.如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).①图2中的阴影部分的面积为(b-a)2;
②观察图2请你写出 (a+b)2、(a-b)2、ab之间的等量关系是(a+b)2-(a-b)2=4ab;
③根据(2)中的结论,若x+y=5,x•y=$\frac{9}{4}$,则(x-y)2=16;
④实际上通过计算图形的面积可以探求相应的等式.
如图3,你发现的等式是(a+b)•(3a+b)=3a2+4ab+b2.
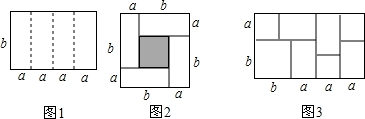
分析 ①表示出阴影部分正方形的边长,然后根据正方形的面积公式列式即可;
②根据大正方形的面积减去小正方形的面积等于四个小长方形的面积列式即可;
③将(x-y)2变形为(x+y)2-4xy,再代入求值即可;
④根据大长方形的面积等于各部分的面积之和列式整理即可.
解答 解:①(b-a)2;
②(a+b)2-(a-b)2=4ab;
③当x+y=5,x•y=$\frac{9}{4}$时,
(x-y)2=(x+y)2-4xy
=52-4×$\frac{9}{4}$
=16;
④(a+b)•(3a+b)=3a2+4ab+b2.
故答案为:①(b-a)2;②(a+b)2-(a-b)2=4ab;③16;④(a+b)•(3a+b)=3a2+4ab+b2.
点评 本题考查了完全平方公式的几何背景,此类题目关键在于同一个图形的面积用两种不同的方法表示.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案
相关题目
1.若a-b=2,ab=3,则ab2-a2b的值为( )
| A. | 6 | B. | 5 | C. | -6 | D. | -5 |
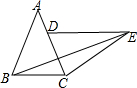 △ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.
△ABC中,∠ABC=∠ACB,将△ABC绕点C顺时针旋转到△EDC,使点B的对应点D落在AC边上,若∠DEB=30°,∠BEC=18°,则∠ABE=36°度.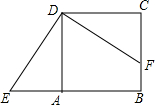 如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.
如图,正方形ABCD中,点F在边BC上,E在边BA的延长线上,△DCF按顺时针方向旋转后恰好与△DAE重合,若AE=3,BF=2,则四边形BFDE的面积是25.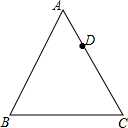 如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.
如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$. 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)