题目内容
18.已知(2x-9)(3x-2)-(3x-2)(x-6)可分解因式为(3x+a)(x-b),其中a、b均为整数,则3a+b的值为( )| A. | -6 | B. | 3 | C. | 9 | D. | -3 |
分析 首先提取公因式(3x-2),即可将原多项式因式分解,继而求得a与b的值,则可求得答案.
解答 解:∵(2x-9)(3x-2)-(3x-2)(x-6)=(3x-2)(2x-9-x+6)=(3x-2)(x-3),
∴a=-2,b=3,
∴3a+b=3×(-2)+3=-3.
故选D.
点评 此题考查了提取公因式法分解因式的知识.注意找到公因式(3x-2)是关键.

练习册系列答案
相关题目
9.(1)一个不透明的盒中装有若干个除颜色外都相同的红球与黄球.在这个口袋中先放入2个白球,再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色后放回盒中,再继续摸球,全班一共做了400次这样的摸球试验.如果知道摸出白球的频数是40,你能估计在未放入白球前,袋中原来共有多少个小球吗?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
由上述的摸球试验推算:
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
(2)提出问题:一个不透明的盒中装有若干个只有颜色不一样的红球与黄球,怎样估算不同颜色球的数量?
活动操作:先从盒中摸出8个球,画上记号放回盒中.再进行摸球试验,摸球试验的要求:先搅拌均匀,每次摸出一个球,记录颜色、是否有记号,放回盒中,再继续摸球、记录、放回袋中.
统计结果:摸球试验活动一共做了50次,统计结果如下表:
| 球的类别 | 无记号 | 有记号 | ||
| 红色 | 黄色 | 红色 | 黄色 | |
| 摸到的次数 | 18 | 28 | 2 | 2 |
①盒中红球、黄球各占总球数的百分比分别是多少?
②盒中有红球多少个?
13.下列图形不是轴对称图形的是( )
| A. | 正方形 | B. | 等腰三角形 | C. | 圆 | D. | 平行四边形 |
10.一元二次方程x2+8x-9=0配方后得到的方程是( )
| A. | (x-4)2+7=0 | B. | (x+4)2=25 | C. | (x-4)2=25 | D. | (x+4)2-7=0 |
8.在平面直角坐标系中,将点(3,2)绕原点O逆时针旋转90°,得到的点的坐标为( )
| A. | (2,-3) | B. | (-2,3) | C. | (-3,2) | D. | (3,-2) |
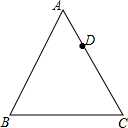 如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$.
如图,点D在边长为6的等边△ABC的边AC上,且AD=2,将△ABC绕点C顺时针方向旋转60°,若此时点A和点D的对应点分别记作点E和点F,联结BF交边AC与点G,那么tan∠AEG=$\frac{3\sqrt{3}}{7}$. 如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)
如图,三个小正方形的边长都为3,则图中阴影部分面积的和是$\frac{27}{8}$π.(结果保留π)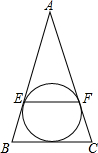 如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.
如图,在△ABC中,AB=AC,它的内切圆分别切AB,AC于点E,F,若AB=100,BC=60,求EF的长.