题目内容
8.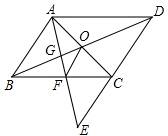 如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.
如图,在?ABCD中,F是边BC的中点,连接AF交DC的延长线于点E,AC,BD相交于点O,AF交BD于点G,连接OF,判断EC与OF的位置关系和大小关系,并证明你的结论.
分析 直接利用平行四边形的性质得出O是AC的中点,进而得出△ABF≌△ECF(ASA),求出答案即可.
解答 解:OF$\stackrel{∥}{=}$$\frac{1}{2}$EC,
理由:∵在?ABCD中,AC,BD相交于点O,
∴O是AC的中点,
又∵F是边BC的中点,
∴FO是△ABC的中位线,
∴OF$\stackrel{∥}{=}$$\frac{1}{2}$AB,
∵AB∥DC,
∴∠ABC=∠BCE,
在△ABF和△ECF中,
$\left\{\begin{array}{l}{∠ABF=∠FCE}\\{BF=FC}\\{∠BFA=∠CFE}\end{array}\right.$,
∴△ABF≌△ECF(ASA),
∴AB=EC,
∴OF$\stackrel{∥}{=}$$\frac{1}{2}$EC.
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质,得出△ABF≌△ECF是解题关键.

练习册系列答案
相关题目
3.矩形ABCD的对角线AC,BD相交于点O,∠AOD=120°,AC=6,则△ABO的周长为( )
| A. | 18 | B. | 15 | C. | 12 | D. | 9 |
18.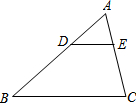 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
 如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若DE=2,BC=5,则AD:DB=( )| A. | 3:2 | B. | 3:5 | C. | 2:5 | D. | 2:3 |
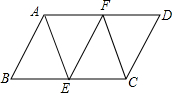 如图,在平行四边形ABCD中,点E、F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )
如图,在平行四边形ABCD中,点E、F分别为边BC,AD的中点,则图中共有平行四边形的个数是( )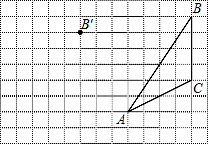 如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和直尺,完成下列各题: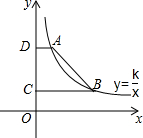 如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4.
如图,点A(2,6),B在反比例函数y=$\frac{k}{x}$(x>0)的图象上,AD⊥y轴于点D,BC⊥y轴于点C,DC=4. 如图,a∥b,∠2=100°,则∠1的度数为80°.
如图,a∥b,∠2=100°,则∠1的度数为80°.