题目内容
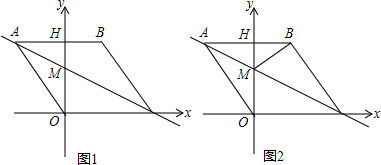
16.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是边长为5的菱形,点C在x轴的正半轴上,直线AC:$y=-\frac{1}{2}x+\frac{5}{2}$交y轴于点M,AB边交y轴于点H.(1)直接写出A、B、C三点坐标;
(2)如图1,动点P从点A出发,沿折线A-B-C方向以2个单位/秒的速度向终点C匀速运动,动点Q同时从点C出发,沿线段AC方向以$\sqrt{5}$个单位/秒的速度向终点A匀速运动,P、Q两点中任意一点到达终点,另一个点随之而停止.设△PQB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)连接BM,如图2,动点P同样从点A出发,沿折线A-B-C方向以2个单位/秒的速度向终点C匀速运动,若tan∠MPB=$\frac{3}{4}$,并求此时直线OP与直线AC所夹锐角的正切值.
分析 (1)由A的坐标求出OA的长,根据四边形ABCO为菱形,利用菱形的四条边相等得到OC=OA,求出OC的长,即可确定出C的坐标;
(2)当点P在线段AB上时,由P的速度为2个单位/秒,时间为t秒,表示出AP,由AB-AP表示出PB,对于直线AC解析式,令x=0,得到y的值,即为OM的长,由OQ-OM求出MQ的长,三角形PBM以PB为底边,MQ为高,表示出S与t的关系式,并求出t的范围即可;当P在线段BC上时,作MQ垂直于BC,由P的速度为2个单位/秒,时间为t秒,表示出AB+BP的长,减去AB表示出BP的长,由四边形ABCO为菱形,利用菱形的性质得到CA为角平分线,利用角平分线定理得到MQ=MO,求出MQ的长,三角形PBM以BP为底边,MQ为高,表示出S与t的关系式,并求出t的范围即可;
(3)根据相似三角形的判定和性质进行解答即可.
解答 解:(1)∵OA=5,
∴A(-3,4),
∵四边形OABC为菱形,
∴OC=OA=5,
∴C(5,0),B(2,4);
(2)①如图1,过Q作QN⊥直线AB于N,
∵A(-3,4),C(5,0),
∴AC=$4\sqrt{5}$,sin∠ACO=$\frac{\sqrt{5}}{5}$,
∵四边形ABCO是边长为5的菱形,
∴sin∠NAQ=sin∠ACO=$\sqrt{5}$$\frac{\sqrt{5}}{5}$,
∵动点Q同时从点C出发,沿线段AC方向以$\sqrt{5}$个单位/秒的速度向终点A匀速运动,
∴AQ=AC-CQ=$4\sqrt{5}$-$\sqrt{5}$t,
∴QN=4-t,
∵动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,
∴PB=5-2t,
∴△PQB的面积为S=$\frac{1}{2}$(5-2t)(4-t)=t2-$\frac{13}{2}$t+10(0≤t≤$\frac{5}{2}$);
②如图2,过Q作QD⊥直线CB于D
∵四边形ABCO是边长为5的菱形,
∴sin∠DCQ=sin∠ACO=$\frac{\sqrt{5}}{5}$,
∵动点Q同时从点C出发,沿线段AC方向以$\sqrt{5}$个单位/秒的速度向终点A匀速运动,
∴CQ=$\sqrt{5}$t,
∴Qd=t,
∵动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,
∴PB=2t-5,
∴△PQB的面积为S=$\frac{1}{2}$(2t-5)t=t2-$\frac{5}{2}$t ($\frac{5}{2}$<t≤4);
(3)①如图3,∵直线AC:$y=-\frac{1}{2}x+\frac{5}{2}$交y轴于点M,
∴OM=$\frac{5}{2}$,
∵四边形ABCO是菱形 A(-3,4),
∴OH=4,AH=3,
∴MH=$\frac{3}{2}$,
∵tan∠MPB=$\frac{3}{4}$,
∴PH=2,
∴AP=1,
∵AB∥OC,
∴△AEP∽△COE,
∴AP:OC=AE:CE=1:5 由(2)①知AC=$4\sqrt{5}$,
∴AE=$\frac{2\sqrt{5}}{3}$,
连结OB交AC于F,
∵四边形ABCO是边长为5的菱形,AC=$4\sqrt{5}$,
∴EF=$\frac{4\sqrt{5}}{3}$,OF=$\sqrt{5}$,
∴直线OP与直线AC所夹锐角∠OEC的正切值是$\frac{3}{4}$;
②∵四边形ABCO是菱形,
∵在△OCM与△BCM中,
$\left\{\begin{array}{l}{OC=BC}\\{∠OCM=∠BCM}\\{CM=CM}\end{array}\right.$,
∴△OCM≌△BCM,
∴BM=OM=$\frac{5}{2}$,∠MBP=∠MOC=90°,
∵tan∠MPB=$\frac{3}{4}$,
∴BP=$\frac{10}{3}$,
∵AO∥BC,
∴△AEO∽△PEC,
∴AE:EC=AO:PC
由(2)①知AC=$4\sqrt{5}$,
∴EF=$\sqrt{5}$,
所以直线OP与直线AC所夹锐角∠OEC的正切值是1.
点评 此题考查了一次函数综合题,涉及的知识有:坐标与图形性质,待定系数法求一次函数解析式,勾股定理,菱形的性质,利用了数形结合及分类讨论的思想,熟练掌握待定系数法是解本题的关键.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案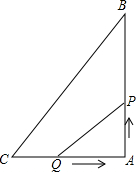 如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒.
如图,在△ABC中,∠BAC=90°,AB=4cm,AC=3cm,动点P、Q分别从点A、C同时出发,点P以2cm/s的速度向终点B移动,点Q以1cm/s的速度向终点A移动,当有一点到达终点时,另一点也停止运动,设运动的时间为t秒. 小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)
小张想测量某建筑物AB的高度,在C处测得建筑物顶部A的仰角为30°,然后沿CB前进100米到达D处,测得顶部A的仰角为60°,求建筑物AB的高度.(结果保留根号)