题目内容
因式分解：a3b+a2-ab3+b2+1．
考点：因式分解-分组分解法
专题：
分析：首先分组进而补项，进而分解因式得出即可．
解答：解：a3b+a2-ab3+b2+1
=a3b-a2b2+a2b2+ab-ab-ab3+a2+b2+1
=a3b-a2b2+ab+a2b2-ab3+b2+a2-ab+1
=ab（a2-ab+1）+b2（a2-ab+1）+（a2-ab+1）
=（a2-ab+1）（ab+b2+1）．
=a3b-a2b2+a2b2+ab-ab-ab3+a2+b2+1
=a3b-a2b2+ab+a2b2-ab3+b2+a2-ab+1
=ab（a2-ab+1）+b2（a2-ab+1）+（a2-ab+1）
=（a2-ab+1）（ab+b2+1）．
点评：此题主要考查了分组分解法分解因式，正确利用补项法分解因式是解题关键．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
已知：在△ABC中，AD为中线，F为AB上一点，CF交AD于E，求证：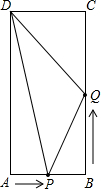
如图，在矩形ABCD中，AB=6cm，BC=8cm，点P从点A沿边AB向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动．
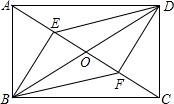如图，在平行四边形ABCD中，∠ABC=90°，对角线AC与BD交于点O，BE⊥AC于E，DF⊥AC于F．