题目内容
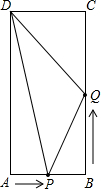 如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm,BC=8cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.(1)当t为何值时,△PBQ的面积为8cm2?
(2)求△ABQ的面积S与运动时间t之间的函数关系.
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)根据运动速度表示出长度和三角形面积公式列出方程.
(2)分别表示出三角形的底和高,利用面积公式列出函数关系式即可.
(2)分别表示出三角形的底和高,利用面积公式列出函数关系式即可.
解答:解:(1)由题意得:
×(6-t)×2t=8
∴t=2或t=4
∴当t=2或t=4时△PBQ的面积等于8cm2.
(2)S△ABQ=
(6-t)×2t=-t2+6t.
| 1 |
| 2 |
∴t=2或t=4
∴当t=2或t=4时△PBQ的面积等于8cm2.
(2)S△ABQ=
| 1 |
| 2 |
点评:考查一元二次方程的应用;表示出所给三角形的两条直角边长是解决本题的突破点;用到的知识点为:直角三角形的面积=两直角边积的一半.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
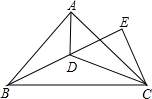 如图,BD、CD平分∠ABC、∠ACB,CE⊥BD交BD延长线于点E,求证:∠DCE=∠CAD.
如图,BD、CD平分∠ABC、∠ACB,CE⊥BD交BD延长线于点E,求证:∠DCE=∠CAD. 如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆.
如图,BD,AH分别是△ABC的高,求证:A、B、H、D四点共圆.