题目内容
4.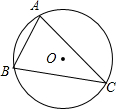 ⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )
⊙O是△ABC的外接圆,⊙O的半径R=2,sinB=$\frac{3}{4}$,则弦AC的长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 3 | D. | $\frac{\sqrt{3}}{2}$ |
分析 连接AO并延长至⊙O于点D,根据直径所对的圆周角为直角,则△ACD为直角三角形;又根据同弧所对的圆周角相等,所以∠B=∠D,则sinD=sinB=$\frac{3}{4}$=$\frac{AC}{AD}$;因为AD=2R=4,所以AC=3.
解答  解:连接AO并延长至⊙O于点D,则△ACD为直角三角形,
解:连接AO并延长至⊙O于点D,则△ACD为直角三角形,
∵∠B=∠D,
∴sinD=sinB=$\frac{3}{4}$=$\frac{AC}{AD}$,
∵AD=2R=4,
∴AC=3.
故选C.
点评 本题重点考查了同弧所对的圆周角相等、直径所对的圆周角为直角及解直角三角形的知识,正确的作出辅助线是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
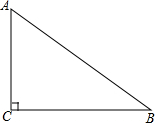 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
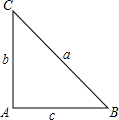 已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.
已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.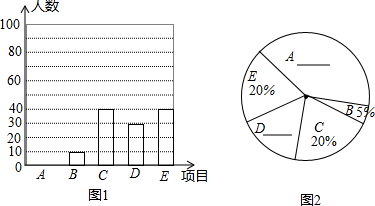
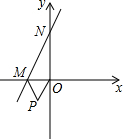 如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.
如图,已知直线y=2x+6与x轴、y轴分别交于M,N两点,以OM为边在x轴下方作等边三角形OMP,现将△OMP沿y轴向上平移,当点P恰好落在直线MN上时,点P运动的路程为$\frac{3}{2}$$\sqrt{3}$+3.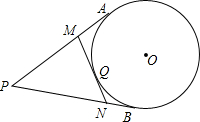 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.