题目内容
19.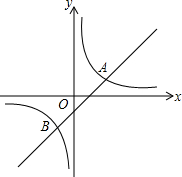 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)(1)b=-1,k=2,
(2)P为x轴上一点,若以A、B、P为顶点的三角形是直角三角形,则点P的坐标为(3,0)、(-3,0)、($\frac{1-\sqrt{17}}{2}$,0)、($\frac{1+\sqrt{17}}{2}$,0).
分析 (1)直接把A点坐标分别代入y=x+b和$y=\frac{k}{x}$中,即可求出b和k的值;
(2)联立方程求得B的坐标,设P点坐标为(t,0),根据两点间的距离公式求得PA2=12+(t-2)2,PB2=22+(t+1)2,AB2=32+32=18,然后分类讨论:①∠APB=90°时,②∠PAB=90°时,③∠PBA=90°时,根据勾股定理得关于t的方程,再分别解方程求出t的值,最后写出P点坐标.
解答 解:(1)把A(2,1)代入y=x+b得1=2+b,解得b=-1;
把A(2,1)代入y=$\frac{k}{x}$得,k=2×1=2;
故答案为-1,2;
(2)解$\left\{\begin{array}{l}{y=x-1}\\{y=\frac{2}{x}}\end{array}\right.$得$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$,
∴A(2,1),B(-1,-2),
设P点坐标为(t,0),
∴PA2=12+(t-2)2,PB2=22+(t+1)2,AB2=32+32=18,
当∠APB=90°时,则PA2+PB2=AB2,即12+(t-2)2+22+(t+1)2=18,解得t=$\frac{1±\sqrt{17}}{2}$,此时P点坐标为($\frac{1-\sqrt{17}}{2}$,0)或($\frac{1+\sqrt{17}}{2}$,0);
当∠PAB=90°时,则PA2+AB2=PB2,即12+(t-2)2+18=22+(t+1)2,解得t=3,此时P点坐标为(3,0);
当∠PBA=90°时,则PB2+AB2=PA2,即22+(t+1)2+18=12+(t-2)2,解得t=-3,此时P点坐标为(-3,0);
综上所述,P点坐标为(3,0)、(-3,0)、($\frac{1-\sqrt{17}}{2}$,0)、($\frac{1+\sqrt{17}}{2}$,0);
故答案为(3,0)、(-3,0)、($\frac{1-\sqrt{17}}{2}$,0)、($\frac{1+\sqrt{17}}{2}$,0).
点评 考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了勾股定理以及分类讨论的思想.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | 无限小数都是无理数 | B. | 实数与数轴上的点一一对应 | ||
| C. | 无理数都是无限小数 | D. | 带有根号的数不都是无理数 |
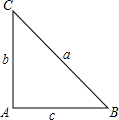 已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.
已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.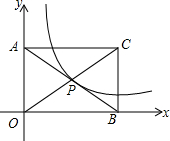 如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$.
如图,矩形AOBC的面积为8,反比例函数y=$\frac{k}{x}$的图象经过矩形对角线的交点P,则反比例函数的解析式为y=$\frac{2}{x}$. 已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.
已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.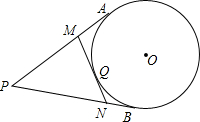 如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.
如图,PA、PB是⊙O的切线,Q为$\widehat{AB}$上一点,过点Q的直线MN与⊙O相切,已知PA=4,则△PMN周长=8.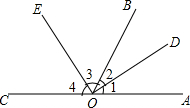 ∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.
∠AOB与∠BOC互为补角,OD平分∠AOB,∠3+∠2=90°,如图所示.求证∠BOE=$\frac{1}{2}$∠BOC.请完成下列证明.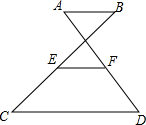 如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长.
如图,AB∥CD,点E是BC的中点,点F是AD的中点,若AB=5,CD=12,求EF的长.