题目内容
19．若正n边形的每个内角都等于120°，其内角和为720°．分析 多边形的内角和可以表示成（n-2）•180°，因为所给多边形的每个内角均相等，故又可表示成120°n，列方程可求解，再利用多边形的内角和定理求解．
解答 解：设所求正n边形边数为n，
则120°n=（n-2）•180°，
解得n=6，
其内角和为（6-2）•180°=720°，
故答案为720°．
点评 本题考查根据多边形的内角和计算公式求多边形的边数，解答时要会根据公式进行正确运算、变形和数据处理．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．△ABC中，AC=4，BC=3，AB=5，tanA的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{3}$ | D． | $\frac{4}{5}$ |
10．
如图所示，该几何体的俯视图是（ ）
如图所示，该几何体的俯视图是（ ）| A． |  | B． |  | C． |  | D． |  |
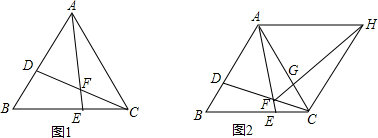
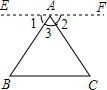已知△ABC，求证∠A+∠B+∠C=180°．请在括号里填上适当的理由．
如图，AB、CD相交于O，OE⊥AB，若∠EOD=70°，则∠AOC=20°．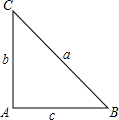
已知△ABC中，∠A=2∠B，∠A=90°，求证：a2-b2=bc．