题目内容
17.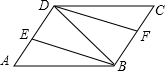 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.(1)求证:△AEB≌△CFD;
(2)若BD=BA,试判断四边形DEBF的形状,并加以证明.
分析 (1)由平行四边形的性质得出AD∥BC,CD∥BA,∠A=∠C,AB=CD,得出∠ABD=∠BDC,由角平分线的定义证出∠DBE=∠FDB,由ASA证明△AEB≌△CFD即可;
(2)先证明四边形DEBF是平行四边形,再根据等腰三角形的“三线合一”的性质推知BE⊥AD,然后由“有一内角为直角的平行四边形是矩形”证得四边形DEBF是矩形即可.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,CD∥BA,∠A=∠C,AB=CD,
∴∠ABD=∠BDC(两直线平行,内错角相等).
又∵BE平分∠ABD,DF平分∠BDC,
∴∠ABE=∠DBE=$\frac{1}{2}$∠ABD,∠CDF=∠BDF=$\frac{1}{2}$∠BDC,
∴∠DBE=∠FDB=∠DBE=∠BDF(等量代换),
在△AEB和△CFD中,$\left\{\begin{array}{l}{∠A=∠C}&{\;}\\{AB=CD}&{\;}\\{∠ABE=∠CDF}&{\;}\end{array}\right.$,
∴△AEB≌△CFD(ASA);
(2)解:四边形DEBF是矩形;理由如下:
由(1)知:∠DBE=∠BDF,
∴BE∥DF,
∵DE∥BF,
∴四边形EBFD是平行四边形.
∵BD=BA,BE是∠ABD的平分线,
∴BE⊥AD,
∴∠DEB=90°,
∴四边形DEBF是矩形(有一内角为直角的平行四边形是矩形).
点评 本题考查矩形的判定与性质,平行四边形的判定与性质,全等三角形的判定与性质,等腰三角形的性质;熟练掌握平行四边形的性质,运用等腰三角形的三线合一性质得出BE⊥AD是解决问题(2)的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB、CD相交于O,OE⊥AB,若∠EOD=70°,则∠AOC=20°.
如图,AB、CD相交于O,OE⊥AB,若∠EOD=70°,则∠AOC=20°.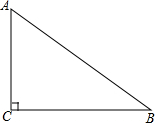 如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )
如图,在Rt△ABC中,∠C=90°,sinB=$\frac{3}{5}$,BC=5cm,以点C为圆心,以3cm的长为半径作圆,则⊙C与AB的位置关系是( )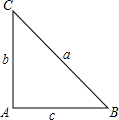 已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc.
已知△ABC中,∠A=2∠B,∠A=90°,求证:a2-b2=bc. 已知:如图,在平行四边形ABCD中,E、F分别是边AB和DC上的点,且BE=DF.求证:AF=CE.
已知:如图,在平行四边形ABCD中,E、F分别是边AB和DC上的点,且BE=DF.求证:AF=CE. 已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.
已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.