题目内容
11.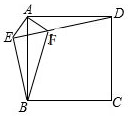 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$(1)求证:△AEB≌△AFD;
(2)试判断EB与ED的位置关系,并说明理由;
(3)求△AEB的面积.
分析 (1)由四边形ABCD是正方形,得到AB=AD,∠BAD=90°,由于AE⊥AF,得到∠EAF=90°,于是得到∠EAB=∠FAD,即可证得△AEB≌△AFD;
(2)由△AEB≌△AFD,得到∠AFD=∠AEB,由于∠AEB=∠AEF+∠BEF,∠AFD=∠AEF+∠FAE,于是得到结论;
(3)如图,过点B作BF⊥AF,交AE延长线于点F.根据△AEP为等腰直角三角形,得到∠AEP=45°,由于∠DEB=90°,得到∠FEB=45°,于是得到△EF′B为等腰角三角形,于是得到FE的长,再由勾股定理得到BE的长,进而求出BF′的长,利用三角形面积公式即可求出△AEB的面积.
解答 解:
(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵AE⊥AF,
∴∠EAF=90°,
∴∠EAB=∠FAD,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{AE=AF}\\{∠EAB=∠FAD}\\{AB=AD}\end{array}\right.$,
∴△AEB≌△AFD;
(2)证明:∵△AEB≌△AFD;,
∴∠AFD=∠AEB,
又∵∠AEB=∠AEF+∠BEF,∠AFD=∠AEF+∠FAE,
∴∠BEF=∠FAE=90°,∴BE⊥DE;
(3)如图,过点B作BF′⊥AF′,交AE延长线于点F′.
∵△AEF为等腰直角三角形,
∴∠AEF=45°,
又∵∠DEB=90°,
∴∠F′EB=45°,
∵∠EF′B=90°,
∴△EF′B为等腰直角三角形,
∵FB=$\sqrt{5}$,EF=$\sqrt{2}$AE=$\sqrt{2}$,
∴BE=$\sqrt{B{F}^{2}-E{F}^{2}}$=$\sqrt{3}$
∴EF′=BF′=$\frac{\sqrt{2}}{2}$BE=$\frac{\sqrt{6}}{2}$,
∴△AEB的面积=$\frac{1}{2}$AE•BF′=$\frac{\sqrt{6}}{4}$.
点评 本题考查了四边形的综合题:熟练掌握正方形的性质、等腰直角三角形的性质和全等三角形的判定与性质以及勾股定理是解题的首要条件;正确的作出辅助线是解题的关键.

 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
| x(亩) | 20 | 25 | 30 | 35 |
| y(元) | 1800 | 1700 | 1600 | 1500 |
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过60亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
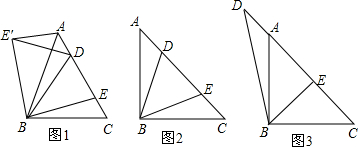
 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )



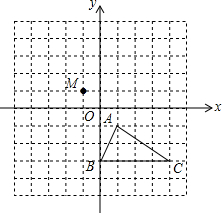 在如图所示的正方形网格中,△ABC的顶点均在格点上,点A的坐标为(1,-1).
在如图所示的正方形网格中,△ABC的顶点均在格点上,点A的坐标为(1,-1).