题目内容
2.在平面直角坐标系中,O为原点,点A(0,2),B(1,1)(1)若点P(m,$\frac{3}{2}$)在线段AB上,求点P的坐标;
(2)以点O,A,B,C(1,0)为顶点的四边形,被直线y=kx-k(k<0)分成两部分,设靠近原点的一侧的面积为s,求s关于k的函数解析式.
分析 (1)根据点A、B的坐标利用待定系数法可求求出直线AB的解析式,将点P的坐标代入直线AB的解析式中即可求出m值,由此即可得出点P的坐标;
(2)由y=kx-k=k(x-1)可知直线y=kx-k过点C(1,0),分0>k≥-2和k<-2两种情况考虑,利用三角形、梯形的面积结合分割图形求面积法即可得出s关于k的函数解析式.
解答 解:(1)设直线AB的解析式为y=kx+b(k≠0),
将A(0,2)、B(1,1)代入y=kx+b,
$\left\{\begin{array}{l}{b=2}\\{k+b=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$,
∴直线AB的解析式为y=-x+2.
∵点P(m,$\frac{3}{2}$)在线段AB上,
∴$\frac{3}{2}$=-m+2,
解得:m=$\frac{1}{2}$.
∴点P的坐标为($\frac{1}{2}$,$\frac{3}{2}$).
(2)依照题意画出图形,如图所示.
∵y=kx-k=k(x-1),
∴直线y=kx-k过点C(1,0).
①当-k≤2,即0>k≥-2时,设直线y=kx-k与y轴的交点为E,
则点E的坐标为(0,-k),
此时s=$\frac{1}{2}$OC•OE=$\frac{1}{2}$×1×(-k)=-$\frac{1}{2}$k;
②当-k>2,即k<-2时,设直线y=kx-k与线段AB的交点为F,
联立直线CF、AB的解析式成方程组,
$\left\{\begin{array}{l}{y=kx-k}\\{y=-x+2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{k+2}{k+1}}\\{y=\frac{k}{k+1}}\end{array}\right.$,
∴点F的坐标为($\frac{k+2}{k+1}$,$\frac{k}{k+1}$),
此时s=$\frac{1}{2}$OC•(OA+BC)-$\frac{1}{2}$BC•(xB-xF)=$\frac{1}{2}$×1×(2+1)-$\frac{1}{2}$×1×(1-$\frac{k+2}{k+1}$)=$\frac{3}{2}$+$\frac{1}{2(k+1)}$.
综上所述:s关于k的函数解析式为s=$\left\{\begin{array}{l}{-\frac{1}{2}k(-2≤k<0)}\\{\frac{3}{2}+\frac{1}{2(k+1)}(k<-2)}\end{array}\right.$.
点评 本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征、三角形的面积以及梯形的面积,解题的关键是:(1)根据点的坐标利用待定系数法求出直线AB的解析式;(2)分0>k≥-2和k<-2两种情况考虑.

 如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.
如图,过四边形ABCD的四个顶点分别作对角线AC,BD的平行线,所围成的四边形EFGH显然是平行四边形.(1)当四边形ABCD分别是菱形、矩形、平行四边形时,相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种?请将你的结论填入下表:
| 四边形ABCD | 菱形 | 矩形 | 平行四边形 |
| 四边形EFGH | 矩形 | 菱形 | 平行四边形 |
| A. | a+2a=3a2 | B. | (-a)3=a3 | C. | a3÷a=3 | D. | a2•a3=a5 |
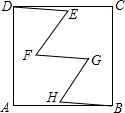 如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.
如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.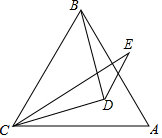 如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.
如图,在△ABC中,AB=AC=BC,在△ABC内取一点D,使DB=DC,又作∠ECD=∠ACD,且AC=EC,试问∠BAC与∠E的数量关系如何?请说明理由.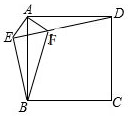 如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$
如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AF⊥AE交DE于点F,已知AE=AF=1,BF=$\sqrt{5}$