题目内容

19．已知P=$\frac{7}{17}$m-1，Q=m2-$\frac{10}{17}$m（m为任意实数），则P与Q的大小关系为（　　）
A．P＞QB．P=QC．P＜QD．不能确定

分析 把P与Q代入Q-P中化简，利用作差法判断即可．

解答 解：∵Q-P=m2-$\frac{10}{17}$m-$\frac{7}{17}$m+1=m2-m+1=（m-$\frac{1}{2}$）2+$\frac{3}{4}$≥$\frac{3}{4}$＞0
∴Q＞P，
故选C

点评 此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．

练习册系列答案
相关题目
19．解方程（组）
（1）$\left\{\begin{array}{l}x-3y=1\\ 2y-x=-5\end{array}\right.$
（2）$\frac{1}{2x-3}$+$\frac{x}{3-2x}$=-2．
20．如图，过四边形ABCD的四个顶点分别作对角线AC，BD的平行线，所围成的四边形EFGH显然是平行四边形．
（1）当四边形ABCD分别是菱形、矩形、平行四边形时，相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种？请将你的结论填入下表：
四边形ABCD菱形矩形平行四边形
四边形EFGH矩形菱形 平行四边形 
（2）反之，当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时，相应的原四边形ABCD必须满足怎样的条件？当对角线互相垂直时，四边形EFGH是矩形；  当对角线相等时四边形EFGH是菱形．
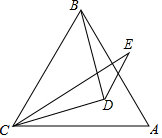7．如图，在△ABC中，AB=AC=BC，在△ABC内取一点D，使DB=DC，又作∠ECD=∠ACD，且AC=EC，试问∠BAC与∠E的数量关系如何？请说明理由．
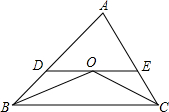14．已知△ABC中，AB=4，AC=8，点D是BC的中点，则AD的取值范围是2＜AD＜6．
4．如图，△ABC中，AB=5，AC=4，BO，CO分别平分∠ABC，∠ACB，过点O作直线平行于BC，交AB、AC于D、E，则△ADE的周长为（　　）
A．8B．9C．10D．12
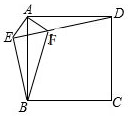11．如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AF⊥AE交DE于点F，已知AE=AF=1，BF=$\sqrt{5}$
（1）求证：△AEB≌△AFD；
（2）试判断EB与ED的位置关系，并说明理由；
（3）求△AEB的面积．
8．（π-3）0+|$\sqrt{2}$-1|-（$\frac{1}{2}$）-2=$\sqrt{2}$-4．
9．下列多项式能因式分解的是（　　）
A．m2+nB．m2-m+nC．m2-2mn+n2D．m2-n

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网