先化简.再求值:$\frac{x-3}{x-2}$÷.其中x=2．题目和参考答案——青夏教育精英家教网—

题目内容

20．先化简，再求值：$\frac{x-3}{x-2}$÷（x+2-$\frac{5}{x-2}}$），其中x=2．

分析原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．

解答解：原式=$\frac{x-3}{x-2}$÷$\frac{{x}^{2}-9}{x-2}$=$\frac{x-3}{x-2}$•$\frac{x-2}{（x+3）（x-3）}$=$\frac{1}{x+3}$，
当x=2时，原式=$\frac{1}{5}$．

点评此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．

练习册系列答案

天利38套中考总复习命题规律与必考压轴题系列答案

相关题目

20．

如图，过四边形ABCD的四个顶点分别作对角线AC，BD的平行线，所围成的四边形EFGH显然是平行四边形．
（1）当四边形ABCD分别是菱形、矩形、平行四边形时，相应的四边形EFGH一定是“平行四边形、菱形、矩形、正方形”中的哪一种？请将你的结论填入下表：

四边形ABCD	菱形	矩形	平行四边形
四边形EFGH	矩形	菱形	平行四边形

（2）反之，当用上述方法所围成的平行四边形EFGH分别是矩形、菱形时，相应的原四边形ABCD必须满足怎样的条件？当对角线互相垂直时，四边形EFGH是矩形；当对角线相等时四边形EFGH是菱形．

11．

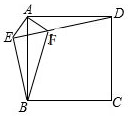如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AF⊥AE交DE于点F，已知AE=AF=1，BF=$\sqrt{5}$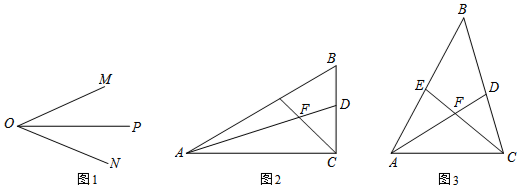
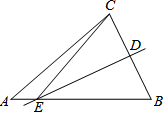（1）求证：△AEB≌△AFD；
（2）试判断EB与ED的位置关系，并说明理由；
（3）求△AEB的面积．

8．（π-3）⁰+|$\sqrt{2}$-1|-（$\frac{1}{2}$）^-2=$\sqrt{2}$-4．

15．（1）如图1，OP是∠MON的平分线，请你在图1中画出一对以OP所在直线为对称轴的全等三角形．
（2）如图2，在△ABC中，∠ACB是直角，∠B=60°，AD、CE分别是∠BAC和∠BCA的平分线，AD、CE相交于点F，请判断写出FE与FD之间的数量关系．
（3）如图3，△ABC中，如果∠ACB不是直角，而（2）中的其他条件不变，AE=3，CD=2，求AC的长度．

5．

如图，在△ABC中，直线ED是线段BC的垂直平分线，直线ED分别交BC、AB于点D、点E，已知BD=4，△ABC的周长为20，则△AEC的周长为（　　）

a²•a³=a⁵

10．运用等式性质的变形，正确的是（　　）

	A．	若2x=a，则x=a-2		B．	若6a=2b，则a=3b
	C．	若a=b+2，则3a=3b+2		D．	若a+c=b+c，则a=b

试题分类