题目内容
4.当x≥1时,不等式|x+1|+$\sqrt{x-1}$≥m-|x-2|恒成立,那么实数m的最大值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 当x≥1时,不等式|x+1|+$\sqrt{x-1}$≥m-|x-2|恒成立,可以得到m≤|x+1|+$\sqrt{x-1}$+|x-2|,然后只要求出|x+1|+$\sqrt{x-1}$+|x-2|的最小值即可求得m的最大值,本题得以解决.
解答 解:∵|x+1|+$\sqrt{x-1}$≥m-|x-2|,
∴m≤|x+1|+$\sqrt{x-1}$+|x-2|,
设y=|x+1|+$\sqrt{x-1}$+|x-2|,
当1≤x<2时,y=x+1+$\sqrt{x-1}$+2-x=3+$\sqrt{x-1}$≥3,
当x≥2时,y=x+1+$\sqrt{x-1}$+x-2=2x+$\sqrt{x-1}$-1≥4,
∴y的最小值是3,
∵当x≥1时,不等式|x+1|+$\sqrt{x-1}$≥m-|x-2|恒成立,
∴m的最大值是3,
故选C.
点评 本题考查绝对值函数的最值,解答此类问题的关键是明确题意,将求m的最大值转化为求|x+1|+$\sqrt{x-1}$+|x-2|的最小值,利用分类讨论的数学思想解答.

练习册系列答案
相关题目
9.已知x,y是实数,$\sqrt{3x+4}$+y2+6y+9=0,若axy-3x=y,则实数a的值是( )
| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{7}{4}$ | D. | -$\frac{7}{4}$ |
16. 如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
 如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )
如图,4个小圆的面积相等,大圆的半径等于小圆的直径,则图中阴影部分的面积S1与大圆的面积S2的大小关系为( )| A. | S1=S2 | B. | S1=$\frac{1}{2}$S2 | C. | S1=$\frac{1}{3}$S2 | D. | S1=$\frac{1}{4}$S2 |

 如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.
如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.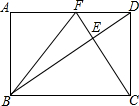 在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.
在矩形ABCD中,DC=2$\sqrt{3}$,CF⊥BD分别交BD、AD于点E、F,连接BF.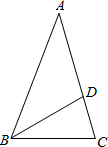 如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.
如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.