题目内容
6. 如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.
如图,Rt△ABC中,∠C=90°,AC=12,BC=9,点P从点A出发,以每秒5个单位的速度向点B匀速运动,同时点Q从点C出发.向点A匀速运动,结果两点同时到目的地.设运动的时间为1.(1)求点Q的运动速度.
(2)当t为何值时,PQ=5?
(3)在点P,Q的运动过程中,求线段PQ中点的运动路径长.
分析 (1)先根据勾股定理,求得AB长,进而得到点P运动到点B所需的时间,最后计算点Q的运动速度即可;
(2)过点P作PD⊥AC于D,则PD∥BC,根据相似三角形的性质,得出PD=3t,AD=4t,再根据CQ=4t,得到DQ=12-4t-4t=12-8t,最后根据勾股定理得到(3t)2+(12-8t)2=52,解得t=1或$\frac{119}{73}$即可;
(3)以A为原点,AC所在直线为x轴,建立平面直角坐标系,当t=0时,点PQ的中点O1的坐标为(6,0),当t=3时,点PQ的中点O2的坐标为(6,$\frac{9}{2}$),进而得到直线O1O2的解析式为x=6,再根据点Q(12-4t,0),P(4t,3t),得到在运动过程中,线段PQ中点O的坐标为($\frac{12-4t+4t}{2}$,$\frac{3}{2}$t),即O(6,$\frac{3}{2}$t),进而得出点O在线段O1O2上,最后根据三角形中位线定理,求得O1O2=$\frac{1}{2}$BC=$\frac{9}{2}$,即可得到线段PQ中点的运动路径长.
解答 解:(1)∵∠C=90°,AC=12,BC=9,
∴Rt△ABC中,AB=$\sqrt{1{2}^{2}+{9}^{2}}$=15,
∴点P运动到点B时,t=$\frac{15}{5}$=3秒,
∴点Q的运动速度=$\frac{12}{3}$=4单位/秒;
(2)如图,过点P作PD⊥AC于D,则PD∥BC,
∴△ADP∽△ACB,
∴AP:AD:DP=AB:AC:BC=5:4:3,
∵AP=5t,
∴PD=3t,AD=4t,
又∵CQ=4t,
∴DQ=12-4t-4t=12-8t,
当PQ=5时,
∵Rt△PDQ中,PD2+DQ2=PQ2,
∴(3t)2+(12-8t)2=52,
解得t=1或$\frac{119}{73}$,
∴当t=1或$\frac{119}{73}$秒时,PQ=5;
(3)如图,以A为原点,AC所在直线为x轴,建立平面直角坐标系,
依题意可知0≤t≤3,
当t=0时,点PQ的中点O1的坐标为(6,0),
当t=3时,点PQ的中点O2的坐标为(6,$\frac{9}{2}$),
∴直线O1O2的解析式为x=6,
∵CQ=4t,AP=5t,
∴AQ=12-4t,AD=4t,PD=3t,
∴点Q(12-4t,0),P(4t,3t),
∴在运动过程中,线段PQ中点O的坐标为($\frac{12-4t+4t}{2}$,$\frac{3}{2}$t),即O(6,$\frac{3}{2}$t),
∴点O在线段O1O2上,
∴即线段PQ中点的运动路径为线段O1O2,
∵P,Q两点同时出发,同时到目的地,
∴O1和O2分别是AC和AB的中点,
∴O1O2=$\frac{1}{2}$BC=$\frac{9}{2}$,
∴线段PQ中点的运动路径长为$\frac{9}{2}$.
点评 本题属于三角形综合题,主要考查了勾股定理,相似三角形的判定与性质,三角形中位线定理以及中点公式的综合应用,解决问题的关键是作辅助线构造相似三角形,运用数形结合思想进行求解.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案| A. | y=$\frac{1}{2}$x+2 | B. | y=2x+4 | C. | y=-2x+2 | D. | y=-$\frac{1}{2}$x+2 |
| A. | 900米 | B. | 1200米 | C. | 1000米 | D. | 1300米 |

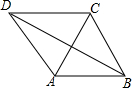 已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.