Question

13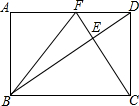．在矩形ABCD中，DC=2$\sqrt{3}$，CF⊥BD分别交BD、AD于点E、F，连接BF．
（1）求证：△DEC∽△FDC；
（2）当F为AD的中点时，求BC的长度．

Answer 1

分析 （1）根据矩形的性质、同角的余角相等得到∠CDE=∠DFE，得到答案；
（2）根据DF∥BC，得到$\frac{FE}{EC}$=$\frac{DF}{BC}$=$\frac{1}{2}$，根据相似三角形的性质得到CE•CF=CD²=12，求出CF，根据勾股定理计算即可．

解答 （1）证明：∵四边形ABCD是矩形，
∴∠FDC=90°，
∴∠FDE+∠CDE=90°，
∵CF⊥BD，
∴∠FDE+∠DFE=90°，
∴∠CDE=∠DFE，又∴∠DEC=∠CDF=90°，
∴△DEC∽△FDC；
（2）解：∵四边形ABCD是矩形，
∴DF∥BC，
∴$\frac{FE}{EC}$=$\frac{DF}{BC}$=$\frac{1}{2}$，
∵△DEC∽△FDC，
∴CE•CF=CD²=12，
∴CF=3$\sqrt{2}$，
∴DF=$\sqrt{C{F}^{2}-C{D}^{2}}$=$\sqrt{6}$，
∴BC=AD=2$\sqrt{6}$．

点评 本题考查的是相似三角形的判定和性质、矩形的性质，掌握相似三角形的判定定理和性质定理是解题的关键．