题目内容
9.已知x,y是实数,$\sqrt{3x+4}$+y2+6y+9=0,若axy-3x=y,则实数a的值是( )| A. | $\frac{1}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{7}{4}$ | D. | -$\frac{7}{4}$ |
分析 利用完全平方公式可得出$\sqrt{3x+4}$+(y+3)2=0,由偶次方和算术平方根的非负性可得出x、y的值,将其代入axy-3x=y中即可求出a值,此题得解.
解答 解:∵$\sqrt{3x+4}$+y2+6y+9=$\sqrt{3x+4}$+(y+3)2=0,
∴3x+4=0,y+3=0,
∴x=-$\frac{4}{3}$,y=-3.
∵axy-3x=y,即4a+4=-3,
解得:a=-$\frac{7}{4}$.
故选D.
点评 本题考查了配方法的应用、偶次方以及算术平方根的非负性,根据偶次方和算术平方根的非负性求出x、y的值是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
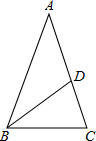 如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.
如图,在△ABC中,AB=AC,∠A=36°,BD是∠ABC的角平分线.
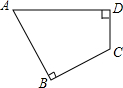 如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.
如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,BC=2,CD=1,求AD的长.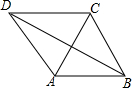 已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.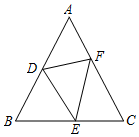 如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.
如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.