题目内容
13.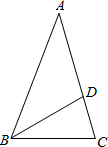 如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.
如图,已知△ABC,AB=AC=2,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是$\sqrt{5}$-1.
分析 证明△DBC∽△BAC,得到点D是AC的黄金分割点,根据黄金分割的概念解答即可.
解答 解:∵∠A=36°,
∴∠ABC=∠ACB=72°,
∵BD是∠ABC的平分线,
∴∠ABD=∠CBD=36°,
∴∠BDC=72°,
∴DA=DB=BC,
∵∠DBC=∠A,∠C=∠C,
∴△DBC∽△BAC,
∴$\frac{BC}{AC}$=$\frac{CD}{BC}$,即BC2=CD•AC,
∴AD2=CD•AC,
∴点D是AC的黄金分割点,
∴AD=$\frac{\sqrt{5}-1}{2}$AC=$\sqrt{5}$-1,
故答案为:$\sqrt{5}$-1.
点评 本题考查的是等腰三角形的性质、相似三角形的判定和性质、黄金分割的概念,掌握黄金比值是$\frac{\sqrt{5}-1}{2}$是解题的关键.

练习册系列答案
相关题目
17.一次函数图象过点(0,2)和(4,0),其函数表达式为( )
| A. | y=$\frac{1}{2}$x+2 | B. | y=2x+4 | C. | y=-2x+2 | D. | y=-$\frac{1}{2}$x+2 |
2.某工程队修一条公路,第一天修了全程的$\frac{1}{3}$,第二天修了余下的40%,还剩下480米没修,这条公路长( )
| A. | 900米 | B. | 1200米 | C. | 1000米 | D. | 1300米 |
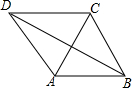 已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.
已知四边形ABCD,AB∥CD,且AB=AC=AD=a,BC=b,且2a>b.求cos∠DBA的值.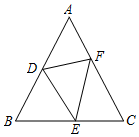 如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF.
如图,△ABC中,∠B=∠C,D、E、F分别在AB、BC、AC上,且∠B=∠DEF,BD=CE,求证:ED=EF. 作出三角形的三条高.
作出三角形的三条高.