题目内容
6.解方程:(1)4-3x=6-5x;
(2)x-$\frac{2x+5}{6}$=1-$\frac{2x-3}{2}$;
(3)-3(2y+2)-2(y-2)=6;
(4)$\frac{x+1}{2}$-1=$\frac{2-x}{3}$.
分析 (1)方程移项合并,把x系数化为1,即可求出解;
(2)方程去分母,去括号,移项合并,把x系数化为1,即可求出解;
(3)方程去括号,移项合并,把y系数化为1,即可求出解;
(4)方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:(1)方程移项合并得:2x=2,
系数化为1得:x=1;
(2)去分母得:6x-(2x+5)=6-3(2x-3),
去括号得:6x-2x-5=6-6x+9,
移项合并得:10x=20,
系数化为1得:x=2;
(3)去括号得:-6y-6-2y+4=6,
移项合并得:-8y=8,
系数化为1得:y=-1;
(4)$\frac{x+1}{2}$-1=$\frac{2-x}{3}$.
去分母得:3(x+1)-6=2(2-x),
去括号得:3x+3-6=4-2x,
移项合并得:5x=7,
系数化为1得:x=1.4.
点评 此题考查了解一元一次方程,其步骤为:去分母,去括号,移项合并,把未知数系数化为1,求出解.

练习册系列答案
相关题目
17.小明在解关于x的方程5a+x=10时,误将“+x”看作“-x”,得方程的解为x=3,则原方程的解为( )
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
14.抛物线y=-5(x-2)2+3的顶点坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
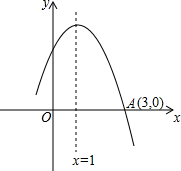 如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( )
如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( )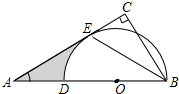 如图,在△ABC中,∠C=90°,D在AB边上,以BD为直径的半圆与AC相切于点E,连接BE.
如图,在△ABC中,∠C=90°,D在AB边上,以BD为直径的半圆与AC相切于点E,连接BE.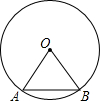 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.
如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.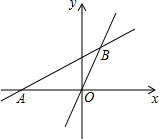 如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.
如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.