题目内容
4.计算:①(-$\frac{2}{3}$)×$\frac{1}{4}$-|-4|3÷(-2)4
②25×$\frac{3}{4}$-(-25)×$\frac{1}{2}$+(-$\frac{1}{4}$)×25.
分析 ①根据有理数的乘法、除法、减法进行计算即可;
②根据有理数的乘除和加减进行计算即可.
解答 解:①(-$\frac{2}{3}$)×$\frac{1}{4}$-|-4|3÷(-2)4
=$-\frac{1}{6}-64×\frac{1}{16}$
=-$\frac{1}{6}-4$
=$-4\frac{1}{6}$;
②25×$\frac{3}{4}$-(-25)×$\frac{1}{2}$+(-$\frac{1}{4}$)×25.
=$\frac{75}{4}+\frac{25}{2}-\frac{25}{4}$
=25.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的法则.

练习册系列答案
相关题目
14.抛物线y=-5(x-2)2+3的顶点坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
19.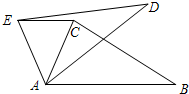 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
13.甲、乙两名队员在相同的条件下各射击10次,每次命中的环数如下表所示:
(1)甲、乙两名队员的射击成绩的平均成绩相等,请补齐甲的成绩;
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲 | 8 | 6 | 7 | 8 | 9 | 10 | 6 | 5 | 4 | 7 |
| 乙 | 7 | 9 | 8 | 5 | 6 | 7 | 7 | 6 | 7 | 8 |
(2)计算甲、乙两名队员的射击成绩的方差;
(3)根据计算结果,评价两名队员的射击情况.
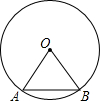 如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.
如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数是30°或150°.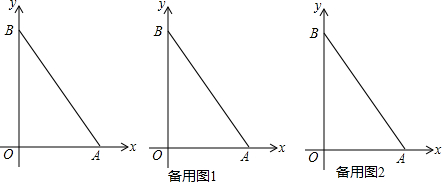
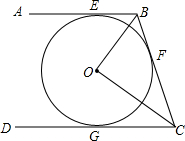 如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB∥CD,BO=6cm,CO=8cm,BC的长为10cm.
如图,AB,BC,CD分别与⊙O相切于E,F,G三点,且AB∥CD,BO=6cm,CO=8cm,BC的长为10cm.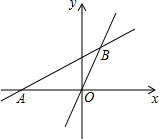 如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.
如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.