题目内容
11.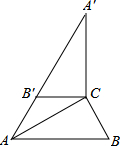 如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为6.
如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为6.
分析 利用直角三角形的性质得出AB=4,再利用旋转的性质以及三角形外角的性质得出AB′=2,进而得出答案.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,
∴∠CAB=30°,故AB=4,
∵△A′B′C由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,
∴AB=A′B′=4,AC=A′C,
∴∠CAA′=∠A′=30°,
∴∠ACB′=∠B′AC=30°,
∴AB′=B′C=2,
∴AA′=2+4=6,
故答案为6.
点评 此题主要考查了旋转的性质以及直角三角形的性质等知识,得出AB′=B′C=1是解题关键,此题难度不大.

练习册系列答案
相关题目
2.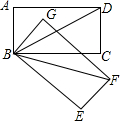 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
 如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )
如图,已知在矩形ABCD中,∠ADB=30°,现将矩形ABCD绕点B顺时针旋转45°到矩形GBEF的位置,则∠CBF的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
19.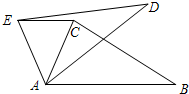 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
 如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )
如图,在△ABC中,∠CAB=65°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC∥AB,则∠BAD的度数为( )| A. | 50° | B. | 40° | C. | 35° | D. | 30° |
20.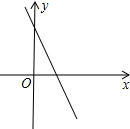 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
 已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )
已知一次函数y=kx+b的图象如图所示,且点(2,m)与(-1,n)都在此函数图象上,则m与n的大小关系为( )| A. | m>n | B. | m<n | C. | m≥n | D. | m≤n |
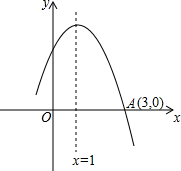 如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( )
如图是函数y=ax2+bx+c图象的一部分,图象与x轴正半轴交于点(3,0),对称轴为直线x=1,则下列结论:①b2>4ac;②当-1<x<3时,ax2+bx+c>0;③无论m为何实数,a+b≥m(ma+b);④若t为方程ax2+bx+c+1=0的一个根,则-1<t<3,其中正确的结论有( ) 一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.
一个几何体由几个大小相同的小立方块搭成,从上面观察这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面、左面看到的这个几何体的形状图.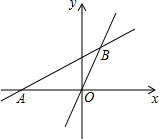 如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.
如图,直线y=$\frac{1}{2}x+\frac{3}{2}$与x轴交于点A,与直线y=2x交于点B.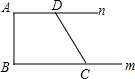 如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$.
如图所示,已知直线m∥n,点A、D在n上,点B、C在m上,且AB⊥n于点A,∠ADC=120°,若CD=6,则AB的长为3$\sqrt{3}$. 如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,
如图,数轴上点A对应的数为a,点B对应的数为b,且a、b满足|2a+6|+3(b-2)2=0,