题目内容
17.将抛物线y=2(x-1)2+1向右平移1个单位长度,再向下移1个单位长度,所得的抛物线解析式为( )| A. | y=2x2+1 | B. | y=2(x-2)2+2 | C. | y=2(x-2)2 | D. | y=2x2 |
分析 先利用顶点式得到抛物线y=2(x-1)2+1的顶点坐标为(1,1),再根据点平移的规律得到点(1,1)平移后对应点的坐标为(2,0),然后根据顶点式写出平移后抛物线解析式.
解答 解:抛物线y=2(x-1)2+1的顶点坐标为(1,1),而点(1,1)向右平移1个单位长度,再向下移1个单位长度,所得对应点的坐标为(2,0),所以所求抛物线解析式为y=2(x-2)2.
故选C.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
12.下列计算正确的是( )
| A. | 2x-3x=x | B. | x2+x3=x5 | C. | x2•x3=x6 | D. | (xy)2=x2y2 |
9.分式方程$\frac{x+1}{{x}^{2}-x}$-$\frac{1}{3x}$=$\frac{x+5}{3x-3}$的解是( )
| A. | x=-4 | B. | x=1 | C. | x1=4,x2=1 | D. | x1=-4,x2=1 |
6.下列函数的图象中,不经过第一象限的是( )
| A. | y=x+3 | B. | y=x-3 | C. | y=-x+1 | D. | y=-x-1 |
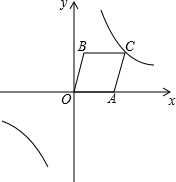 如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.
如图,A(4,0),B(1,3),以OA、OB为边作平行四边形OACB,反比例函数y=$\frac{k}{x}$的图象经过点C.