题目内容
9.分式方程$\frac{x+1}{{x}^{2}-x}$-$\frac{1}{3x}$=$\frac{x+5}{3x-3}$的解是( )| A. | x=-4 | B. | x=1 | C. | x1=4,x2=1 | D. | x1=-4,x2=1 |
分析 先确定分式方程的最简公分母,约去分母,把分式方程化为整式方程,求出x的值,再把x的值代入3x(x-1)进行检验即可.
解答 解:方程两边同时乘以3x(x-1)得3(x+1)-(x-1)=x(x+5)
整理得x2+3x-4=0
解得:x1=-4,x2=1
检验:当x=-4时3x(x-1)≠0,x=1时3x(x-1)=0,
因此x=-4是原分式方程的解.
故选:A.
点评 本题主要考查的是分式方程的解法,解分式方程的步骤为:方程两边同乘最简公分母约去分母化为整式方程,解整式方程,将整式方程的解代入最简公分母检验确定分式方程的根.

练习册系列答案
相关题目
19.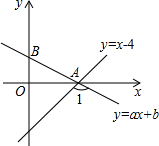 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )| A. | y=-$\frac{1}{2}$x+2 | B. | y=$\frac{1}{2}$x+2 | C. | y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$ |
17.将抛物线y=2(x-1)2+1向右平移1个单位长度,再向下移1个单位长度,所得的抛物线解析式为( )
| A. | y=2x2+1 | B. | y=2(x-2)2+2 | C. | y=2(x-2)2 | D. | y=2x2 |
14.如图几何体中的左视图不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |