题目内容

2．从一副没有“大小王”的扑克牌中随机抽取一张点数为8的扑克，其概率是$\frac{1}{13}$．

分析 让点数为8的扑克牌的张数除以没有大小王的扑克牌总张数即为所求的概率．

解答 解：∵没有大小王的扑克牌共52张，其中点数为8的扑克牌4张，
∴随机抽取一张点数为8的扑克，其概率是$\frac{4}{52}$=$\frac{1}{13}$．
故答案为$\frac{1}{13}$．

点评 本题考查的是随机事件概率的求法，如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．

练习册系列答案
相关题目
12．下列各式的计算过程及结果都正确的是（　　）
A．$\frac{y}{5x}÷\frac{1}{3}x=\frac{y}{5x}•3x=\frac{3}{5}y$
B．$8xy÷\frac{4x}{y}=\frac{1}{8xy}•\frac{4x}{y}=\frac{1}{2{y}^{2}}$
C．$\frac{x}{2a}÷\frac{2b}{y}=\frac{x}{2a}•\frac{y}{2b}=\frac{xy}{2ab}$
D．$\frac{x+y}{{x}^{2}-xy}÷\frac{1}{x-y}=\frac{x+y}{x（x-y）}•（x-y）=\frac{x+y}{x}$
13．若代数式$\frac{1}{\sqrt{x+2}}$有意义，则实数x的取值范围是（　　）
A．x≥-2B．x＞-2C．x≤-2D．x＜-2
10．-3的相反数是（　　）
A．±3B．3C．-3D．$\frac{1}{3}$
17．将抛物线y=2（x-1）2+1向右平移1个单位长度，再向下移1个单位长度，所得的抛物线解析式为（　　）
A．y=2x2+1B．y=2（x-2）2+2C．y=2（x-2）2D．y=2x2
7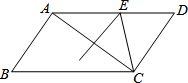．如图，在平行四边形ABCD中，AB=8，BC=12，AC的垂直平分线交AD于点E，则△CDE的周长是（　　）
A．14B．20C．22D．24
14．如图几何体中的左视图不是中心对称图形的是（　　）
A．B．C．D．
11．已知关于x的二次函数y=x2+（k2-3k-4）x+2k的图象与x轴从左到右交于A，B两点，且这两点关于原点对称．
（1）求k的值；
（2）在（1）的条件下，若反比例函数y=$\frac{m}{x}$的图象与二次函数y=x2+（k2-3k-4）x+2k的图象从左到右交于Q，R，S三点，且点Q的坐标为（-1，-1），点R（xR，yR），S（xs，ys）中的纵坐标yR，ys分别是一元二次方程y2+my-1=0的解，求四边形AQBS的面积S四边形AQBS；
（3）在（1），（2）的条件下，在x轴下方是否存在二次函数y=x2+（k2-3k-4）x+2k图象上的点P使得S△PAB=2S△RAB？若存在，求出点P的坐标；若不存在，请说明理由．
12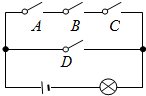．如图，电路图上有四个开关A、B、C、D和一个小灯泡，闭合开关D或同时闭合开关A、B、C都可使小灯泡发光，则任意闭合其中两个开关，小灯泡发光的概率是（　　）
A．$\frac{1}{2}$B．$\frac{2}{3}$C．$\frac{1}{4}$D．$\frac{2}{5}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网