Question

2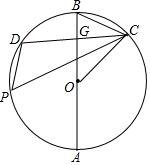．在⊙O中，直径AB⊥CD于点G（CD为非直径弦），P是⊙O上一动点（不考虑点P与C，D重合的情况）
（1）当点P在$\widehat{DAC}$上时，求证：∠CPD=∠COB；
（2）当点P运动到什么位置时，△CPD∽△BOC？请说明理由；
（3）在（2）的情况下，当∠COB=30°，求$\frac{tan15°}{2-\sqrt{3}}$的值．

Answer 1

分析 （1）连接PB，由垂径定理和圆周角定理即可证明∠CPD=∠COB；
（2）当点P运动到点A时△CPD∽△BOC，连接AD，AC根据圆周角定理证明∠PDC=∠OBC即可；
（3）由已知条件可知∠BAC=15°，设CG=x，在直角三角形AGC中，求出tan15°的值，即可求出$\frac{tan15°}{2-\sqrt{3}}$的值．

解答 解：
（1）证明：连接PB，
∵直径AB⊥CD于点G（CD为非直径弦），
∴$\widehat{BC}=\widehat{BD}$，
∴∠BPC=∠BPD，
∴∠DPC=2∠BPC，
∵∠COB=2∠BPC，
∴∠CPD=∠COB；

（2）当点P运动到点A时△CPD∽△BOC，理由如下：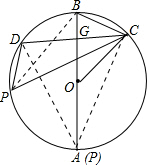
连接AD，AC，
∵直径AB⊥CD于点G，
∴DG=CG，
∴AD=AC，
∴∠ADC=∠ACD，
∵OB=OC，
∴∠OBC=∠OCB，
又∵∠ADC=∠OBC，
∴∠ADC=∠ACD=∠OBC=∠OCB，
∴△CPD∽△BOC；
（3）∵OC=OA，
∴∠OCA=∠OAC，
∵∠COB=30°，
∴∠OAC=15°，
设CG=x，
∵直径AB⊥CD于点G，∠COB=30°，
∴OC=OA=2x，
∴OG=$\sqrt{3}$x，
在直角三角形AGC中，tan15°=$\frac{CG}{AG}=\frac{x}{\sqrt{3}x+2x}$=2-$\sqrt{3}$，
∴$\frac{tan15°}{2-\sqrt{3}}$=$\frac{2-\sqrt{3}}{2-\sqrt{3}}$=1．

点评 本题考查了和圆有关的综合性题目，用到的知识点有垂径定理、圆周角定理、等腰三角形的判断和性质、相似三角形的判断和性质以及锐角三角函数的定义，正确求出tan15°的值是解题的关键．