题目内容
12.已知实数x1,x2满足x1+x2=11,x1x2=30,则以x1,x2为根的一元二次方程是( )| A. | x2-11x+30=0 | B. | x2+11x+30=0 | C. | x2+11x-30=0 | D. | x2-11x-30=0 |
分析 根据根与系数的关系结合两根之和及两根之积的值即可得出$\frac{b}{a}$=-11、$\frac{c}{a}$=30,当a=1时,即可找出b、c的值,此题得解.
解答 解:∵实数x1,x2满足x1+x2=11,x1x2=30,
∴一元二次方程中:$\frac{b}{a}$=-11,$\frac{c}{a}$=30.
当a=1时,b=-11,c=30.
故选A.
点评 本题考查了根与系数的关系,根据两实数之和与之积的值找出$\frac{b}{a}$=-11、$\frac{c}{a}$=30是解题的关键.

练习册系列答案
相关题目
2. 如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )
如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )
 如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )
如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO的度数是( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
3.在二次根式$\sqrt{x-2}$中,字母x的取值范围是( )
| A. | x>2 | B. | x<2 | C. | x≥2 | D. | x≤2 |
20.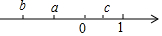 有理数a,b,c在数轴上的位置如图所示,则化简|a+b|-|b-1|-|a-c|-|1-c|得到的结果是( )
有理数a,b,c在数轴上的位置如图所示,则化简|a+b|-|b-1|-|a-c|-|1-c|得到的结果是( )
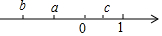 有理数a,b,c在数轴上的位置如图所示,则化简|a+b|-|b-1|-|a-c|-|1-c|得到的结果是( )
有理数a,b,c在数轴上的位置如图所示,则化简|a+b|-|b-1|-|a-c|-|1-c|得到的结果是( )| A. | 0 | B. | -2 | C. | 2a | D. | 2c |
7.在数轴上表示下列各数的点与表示-1的点距离最近的是( )
| A. | -1.75 | B. | -1.5 | C. | -0.25 | D. | -1.25 |
4.化简$\frac{3+a}{2a-4}$÷$\frac{{a}^{2}-9}{a-2}$的结果为( )
| A. | $\frac{1}{2a-6}$ | B. | $\frac{1}{a-3}$ | C. | $\frac{1}{2a+6}$ | D. | $\frac{1}{a+3}$ |
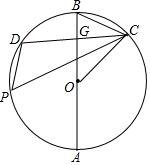 在⊙O中,直径AB⊥CD于点G(CD为非直径弦),P是⊙O上一动点(不考虑点P与C,D重合的情况)
在⊙O中,直径AB⊥CD于点G(CD为非直径弦),P是⊙O上一动点(不考虑点P与C,D重合的情况)