题目内容
14．
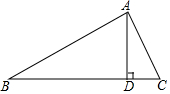如图，在△ABC中，AB=25，AC=17，边BC上的高AD=15cm，求△ABC的面积．
分析 直接利用勾股定理得出DC，DB的长，再利用三角形面积求法得出答案．
解答 解：∵在Rt△ADC中，AC=17，AD=15，
∴DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=8，
在Rt△ABD中，
∵AB=25，AD=15，
∴BD=$\sqrt{2{5}^{2}-1{5}^{2}}$=20，
∴BC=28，
∴△ABC的面积为：$\frac{1}{2}$×28×15=210．
点评 此题主要考查了勾股定理以及三角形面积求法，正确得出DC，BD的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在正方形纸片ABCD中，对角线AC、BD交于点O，折叠正方形纸片ABCD，使AD落在BD上，点A恰好与BD上的点F重合，展开后，折痕DE分别交AB、AC于点E、G，连接GF，下列结论中正确的是①②③．（填序号）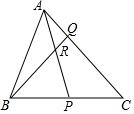 
图中，AQC及BPC均为直线，AP为△ABC的一条角平分线，而BQ为△ABC的一条顶垂线，AP与BQ相交于R．若∠ABC=64°及∠ACB=46°，求∠PRQ．
19．
如图，△ABC和△DCE都是边长为4的等边三角形，点B，C，E在同一条直线上，连接BD，则BD长（ ）
如图，△ABC和△DCE都是边长为4的等边三角形，点B，C，E在同一条直线上，连接BD，则BD长（ ）| A． | 3 | B． | 2$\sqrt{3}$ | C． | 3$\sqrt{3}$ | D． | 4$\sqrt{3}$ |