题目内容
6.已知在平面直角坐标系中,O为坐标原点,点A的坐标为(2,a),点B的坐标为(b,2),点C的坐标为(c,0),其中a,b满足(a+b-10)2+|a-b+2|=0.(1)求A,B两点的坐标;
(2)当△ABC的面积为10时,求点C的坐标;
(3)当2≤S△ABC≤12时,则点C的横坐标c的取值范围是-2≤c≤8或12≤c≤22.
分析 (1)根据非负数的性质即可得到A点的坐标(2,4),B点的坐标(6,2);
(2)求得直线AB与x轴的交点为D(10,0),于是得到S△ABC=S△ACD-S△BCD,列方程即可得到结论;
(3)根据已知条件列方程即可得到结论.
解答 解:(1)∵(a+b-10)2+|a-b+2|=0,
∴(a+b-10)2=0,|a-b+2|=0,
解得:a=4,b=6,
∴A点的坐标(2,4),B点的坐标(6,2);
(2)∵A点的坐标(2,4),B点的坐标(6,2),
∴直线AB的解析式为:y=-$\frac{1}{2}$x+5,
当y=0时,x=10,
∴直线AB与x轴的交点为D(10,0),
∴S△ABC=S△ACD-S△BCD,
∵点C的坐标为(c,0),
∴$\frac{1}{2}$×(10-c)×4-$\frac{1}{2}$(10-c)×2=10或$\frac{1}{2}$×(c-10)×4-$\frac{1}{2}$(c-10)×2=10
解得:c=0,或c=20,
∴点C的坐标(0,0)或(20,0);
(3)由(2)知,①$\frac{1}{2}$×(10-c)×4-$\frac{1}{2}$(10-c)×2=2或$\frac{1}{2}$×(c-10)×4-$\frac{1}{2}$(c-10)×2=2,
解得:c=8或12,
②$\frac{1}{2}$×(10+c)×4-$\frac{1}{2}$(10+c)×2=12或$\frac{1}{2}$×(|c|-10)×4-$\frac{1}{2}$(c-10)×2=12,
解得:c=-2或c=22,
∴当2≤S△ABC≤12时,则点C的横坐标c的取值范围是-2≤c≤8或12≤c≤22,
故答案为-2≤c≤8或12≤c≤22.
点评 本题考查了坐标与图形旋转,非负数的性质,解方程,三角形的面积的计算,正确的理解题意是解题的关键.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案| A. | a≥-1 | B. | a>-1 | C. | a≥0 | D. | a为任意实数 |
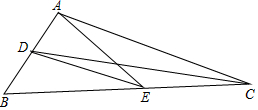 如图所示,在△ABC中,∠BAC=100°,∠ACB=30°,∠EAC=20°,CD平分∠ACB,则∠DEB的度数是25°.
如图所示,在△ABC中,∠BAC=100°,∠ACB=30°,∠EAC=20°,CD平分∠ACB,则∠DEB的度数是25°.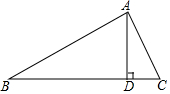 如图,在△ABC中,AB=25,AC=17,边BC上的高AD=15cm,求△ABC的面积.
如图,在△ABC中,AB=25,AC=17,边BC上的高AD=15cm,求△ABC的面积.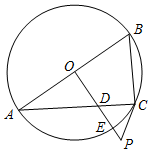 如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.