题目内容
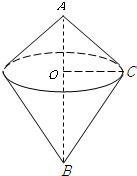
在直角三角形中两直角边分别长3厘米和4厘米,斜边长5厘米,则分别以一边所在直线为轴旋转一周,得到的三个几何体的体积有何关系.
考点:点、线、面、体,圆锥的计算
专题:
分析:根据点动成线,线动成面,面动成体系的道理,一个直角三角形绕一条直角边旋转一同,将会得到一个以旋转的直角边为高,另一直角边为底面半径的圆锥,根据根据圆锥的体积公式V=
πr2h即可分别求出这每个圆锥的体积.以斜边所在直线为轴旋转一周,几何体的体积是由上下两个圆锥的体积组成的,它们的底面半径相同,都是直角三角形斜边上的高,利用圆锥体积公式,即可求得结论.
| 1 |
| 3 |
解答:解:以4厘米的直角边为轴旋转:
体积为:
×3.14×32×4
=
×3.14×9×4
=37.68(立方厘米);
以3厘米的直角边为轴旋转:
 体积为:
体积为:
×3.14×42×3
=
×3.14×16×3
=50.24(立方厘米);
如图,斜边的高为:3×4÷5=
(厘米),
以AC为母线的圆锥体积=
π•(
)2•AO,
以BC为母线的圆锥体积=
π•(
)2•BO,
则绕斜边旋转一周形成的几何体的体积为:
π•(
)2•AB=
πcm3.
体积为:
| 1 |
| 3 |
=
| 1 |
| 3 |
=37.68(立方厘米);
以3厘米的直角边为轴旋转:
 体积为:
体积为:| 1 |
| 3 |
=
| 1 |
| 3 |
=50.24(立方厘米);
如图,斜边的高为:3×4÷5=
| 12 |
| 5 |
以AC为母线的圆锥体积=
| 1 |
| 3 |
| 12 |
| 5 |
以BC为母线的圆锥体积=
| 1 |
| 3 |
| 12 |
| 5 |
则绕斜边旋转一周形成的几何体的体积为:
| 1 |
| 3 |
| 12 |
| 5 |
| 48 |
| 5 |
点评:本题考查的知识有:直角三角形的特征、圆锥的特征、圆锥体积的计算.求圆锥的体积关键是弄清圆锥的底面半径和高.

练习册系列答案
相关题目
 已知在△ABC中,
已知在△ABC中,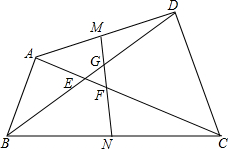 如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.
如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.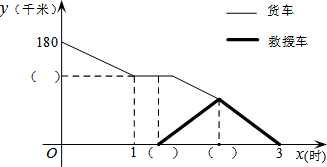 甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计).
甲地与乙地相距180千米.一辆装载物资的货车从甲地开往乙地,在行驶途中突发故障,司机马上通报乙地并立即维修.12分钟后,乙地派出救援车前往接应.经过抢修,货车在救援车出发8分钟后修复并继续按原速行驶.当两车在途中相遇时,为了确保物资能准时运到,将物资全部转移到救援车上,救援车沿原路按原速返回,并按货车的预计时间到达乙地.下图是货车、救援车距乙地的距离y(千米)与货车出发时间x(时)之间的函数图象(装卸货物时间忽略不计).