题目内容
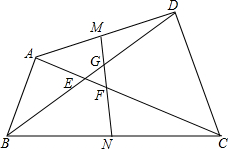 如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.
如图,BD=AC,M、N分别为AD、BC的中点,AC、BD交于E,MN与BD、AC分别交于点F、G,求证:EF=EG.考点:三角形中位线定理
专题:证明题
分析:取CD的中点H,连接MH、NH,根据三角形的中位线平行于第三边并且等于第三边的一半可得MH∥AC,MH=
AC,NH∥BD,NH=
BD,然后求出MH=NH,∠MNH=∠EGF,∠NMH=∠EFG,根据等边对等角可得∠MNH=∠NMH,从而得到∠EFG=∠FGE,再根据等角对等边可得EF=FG.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 证明:如图,取CD的中点H,连接MH、NH,
证明:如图,取CD的中点H,连接MH、NH,
∵M、N分别为AD、BC的中点,
∴MH、NH分别是△ACD和△BCD的中位线,
∴MH∥AC,MH=
AC,NH∥BD,NH=
BD,
∴∠MNH=∠EGF,∠NMH=∠EFG,
又∵BD=AC,
∴MH=NH,
∴∠MNH=∠NMH,
∴∠EFG=∠FGE,
∴EF=EG.
 证明:如图,取CD的中点H,连接MH、NH,
证明:如图,取CD的中点H,连接MH、NH,∵M、N分别为AD、BC的中点,
∴MH、NH分别是△ACD和△BCD的中位线,
∴MH∥AC,MH=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MNH=∠EGF,∠NMH=∠EFG,
又∵BD=AC,
∴MH=NH,
∴∠MNH=∠NMH,
∴∠EFG=∠FGE,
∴EF=EG.
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等边对等角的性质,熟记定理和性质是解题的关键,难点在于作辅助线构造出三角形的中位线.

练习册系列答案
相关题目
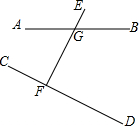 如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=
如图,直线AB、CD被EF所截,交点分别为G、F,∠CFG=∠DFG=
 如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.
如图,△ABC两个外角∠CBD、∠BCE的平分线相交于点O,∠A=40°,求∠BOC的度数.