题目内容
已知二次函数y=ax2+bx+c的图象过点A(0,3),它的对称轴为x=2且方程ax2+bx+c=0的两实根的平方和为10,求二次函数的解析式.
考点:抛物线与x轴的交点
专题:
分析:把点(0,3)代入函数解析式求得c=3;再根据对称轴为x=2,可得-
=2;设方程的2个根分别为m、n,则由韦达定理以及m2+n2=16-
=10,求得a和b的值,从而求得二次函数的解析式.
| b |
| 2a |
| 6 |
| a |
解答:解:把点(0,3)代入函数y=ax2+bx+c(a≠0),可得c=3.
再根据对称轴为x=2,可得-
=2.
设方程的2个根分别为m、n,则由韦达定理可得 m+n=-
=4,mn=
,
再由m2+n2=(m+n)2-2mn=16-
=10,
求得a=1,
则b=-4,
抛物线解析式为:y=x2-4x+3.
再根据对称轴为x=2,可得-
| b |
| 2a |
设方程的2个根分别为m、n,则由韦达定理可得 m+n=-
| b |
| a |
| 3 |
| a |
再由m2+n2=(m+n)2-2mn=16-
| 6 |
| a |
求得a=1,
则b=-4,
抛物线解析式为:y=x2-4x+3.
点评:此题主要考查了抛物线与x轴交点问题,由韦达定理可得 m+n=-
=4,mn=
是解题关键.
| b |
| a |
| 3 |
| a |

练习册系列答案
相关题目
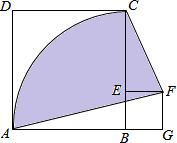 如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )
如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为( )| A、2π | B、4π |
| C、4π-2 | D、6π |
