题目内容
4.我们学过圆内接四边形,学会了它的性质;圆内接四边形对角互补.下面我们进一步研究.(1)在图(1)中.∠ECD是圆内接四边形ABCD的-个外角.请你探究∠DCE与∠A的关系.并说明理由.
(2)请你应用上述结论解答下题:如图(2)已知ABCD是圆内接四边形,F、E分别为BD,AD 延长线上的点.如果DE平分∠FDC.求证:AB=AC.
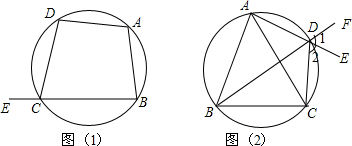
分析 (1)根据圆内接四边形的对角互补和邻补角的定义证明结论;
(2)根据圆内接四边形的性质和圆周角定理证明∠ABC=∠ACB,根据等角对等边得到答案.
解答 解:(1)∠DCE=∠A,
∵∠A+∠DCB=180°,
∠DCE+∠DCB=180°,
∴∠DCE=∠A;
(2)∵已知ABCD是圆内接四边形,
∴∠ABC=∠2,
∠ADB=∠ACB,∠ADB=∠1,
∠ACB=∠1,
∵DE平分∠FDC,
∴∠1=∠2,
∴∠ABC=∠ACB,
∴AB=AC.
点评 本题考查的是圆内接四边形的性质,掌握圆内接四边形的对角互补是解题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
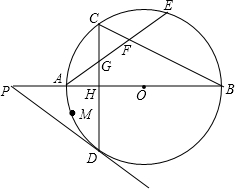 如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F.
如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F. 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则不等式ax2+bx+c<0的解集是-1<x<3.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则不等式ax2+bx+c<0的解集是-1<x<3.