题目内容
7. △ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.
△ABC中,∠ABC=120°,以AC为边向形外作等边三角形ACD,求证:BD=AB+BC.
分析 延长AB到点E,使BE=BC,连接CE,得到△BCE是等边三角形证明△ACE≌△BCE,得到BD=AE,根据AE=AB+BE,所以BD=AB+BC.
解答 解:延长AB到点E,使BE=BC,连接CE,
∵∠ABC=120°
∴∠CBE=60°
∴△BCE是等边三角形
∴CE=CB,∠BCE=60°
∵∠ACD=60°
∴∠BCD=∠ACE,
∵△ACD为等边三角形,
∴CA=CD,
在△ACE和△BCE中,
$\left\{\begin{array}{l}{CE=CB}\\{∠ACE=∠BCD}\\{CA=CD}\end{array}\right.$
∴△ACE≌△DCB,
∴BD=AE,
∵AE=AB+BE,
∴BD=AB+BC.
点评 本题考查了等边三角形的性质、全等三角形的性质与判定,解决本题的关键是作出辅助线,证明△ACE≌△BCE.

练习册系列答案
相关题目
11.在△ABC中,点I是内心,∠BIC=114°,则∠A的度数为( )
| A. | 57° | B. | 66° | C. | 48° | D. | 78° |
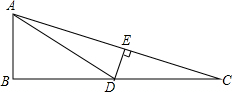 如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度.
如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度. 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.