题目内容
15.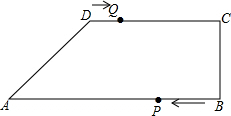 四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.
四边形ABCD中,AB∥CD,CB⊥CD,AB=18cm,BC=6cm,CD=10cm,点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,P,Q两点同时开始运动.设运动时间为T秒.(1)PB=2t,DQ=t
(2)T取何值时,四边形APQD为平行四边形.
(3)直接指出T取何值时,四边形BCQP为矩形?
(4)当T=4时,四边形APCD是什么特殊的四边形?请说明理由.
分析 (1)直接用t表示出PB及DQ的长即可;
(2)根据平行四边形的对边相等即可得出结论;
(3)根据CQ=PB时四边形BCQP为矩形可得出T的值;
(4)过点D作DE⊥AB于点E,连接PC,先根据勾股定理求出DE及AE的长,进而得出PC的长,由此可得出结论.
解答 解:(1)∵点P在线段BA上从B向A运动,速度为2cm/s,点Q在线段DC上从D向C运动,速度为1cm/s,
∴PB=2T,DQ=T.
故答案为:2T,T;
(2)∵四边形APQD为平行四边形,
∴AP=DQ,即18-2T=T,解得T=6(秒).
答:T等于6秒时,四边形APQD为平行四边形;
(3)∵AB∥CD,CB⊥CD,
∴CQ=PB时四边形BCQP为矩形,即10-T=2T,解得T=$\frac{10}{3}$(秒).
答:T为$\frac{10}{3}$秒时,四边形BCQP为矩形;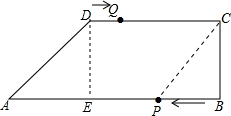
(4)过点D作DE⊥AB于点E,连接PC,
∵AB=18cm,BC=6cm,CD=10cm,
∴AE=18-10=8cm,
∴AD=$\sqrt{{AE}^{2}+{DE}^{2}}$=$\sqrt{{8}^{2}+{8}^{2}}$=8$\sqrt{2}$cm.
∵T=4秒,
∴AP=18-8=10cm,
∴CD=AP,
∴四边形APCD是平行四边形.
点评 本题考查的是四边形综合题,涉及到矩形、平行四边形的判定与性质等知识,在解答(3)时要注意作出辅助线,利用勾股定理求解,此题难度适中.

练习册系列答案
相关题目
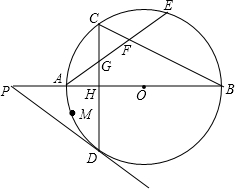 如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F.
如图,AB是⊙O的直径,弦CD⊥AB于H,点E在$\widehat{BC}$上,且$\widehat{CE}=\widehat{AD}$,AE与CD交于点G,与BC交于点F. 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.