题目内容
5.如图Rt△ABC,AC=BC=8,正方形DEFG的边长为2,把正方形DEFG按如图1位置摆放(点E与点B重合,其中F、E、B、C在同一直线上).M为线段AC的中点,正方形DEFG按如图1的起始位置沿射线BM的方向以每秒$\sqrt{5}$个单位长度的速度匀速移动,设移动的时间为t秒.当点F在线段AC上时,正方形DEFG停止移动(如图2).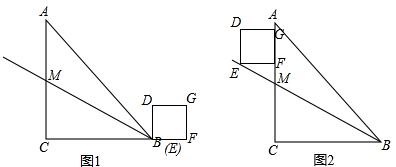
(1)正方形DEFG移动多少秒时,点D在线段AB上;
(2)在移动过程中,正方形DEFG和△ABM重叠部分的面积为S,请直接写出面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围;
(3)如图2,当点F在AC上时,将正方形DEFG沿CA平移至点G与点A重合,将正方形DEFG绕点A旋转,在旋转过程中,设直线DE交射线BA于点P,交射线BC于点Q,当△BPQ为等要直角三角形时,求BP的长.
分析 (1)首先根据DE∥AM,可得△BDE∽△BAM,所以$\frac{BE}{BM}=\frac{DE}{AM}$,据此求出BE的值;然后用BE的值除以正方形DEFG运动的速度,求出正方形DEFG移动多少秒时,点D在线段AB上即可.
(2)根据题意,分3种情况:①当0≤t≤2时;②当2<t≤4时;③当4<t≤5时,求出面积S与运动时间t之间的函数关系式,并写出自变量t的取值范围即可.
(3)根据题意,分4种情况:①当旋转角为0°时;②当旋转角为45°时;③当旋转角为180°时;④当旋转角为225°时;分类讨论,求出BP的长是多少即可.
解答 解:(1)如图1,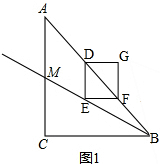 ,
,
∵Rt△ABC,AC=BC=8,M为线段AC的中点,
∴AM=CM=8÷2=4,
再Rt△BCM中,
BM=$\sqrt{{BC}^{2}{+CM}^{2}}$=$\sqrt{{8}^{2}{+4}^{2}}=4\sqrt{5}$,
∵DE∥AM,
∴△BDE∽△BAM,
∴$\frac{BE}{BM}=\frac{DE}{AM}$,
∴$\frac{BE}{4\sqrt{5}}=\frac{2}{4}$,
解得BE=2$\sqrt{5}$,
∴t=2$\sqrt{5}÷\sqrt{5}$=2,
即正方形DEFG移动2秒时,点D在线段AB上.
(2)①当0≤t≤2时,如图2,DE交AB于点P,EF交AB于点Q,作MN∥BC交AB于点N,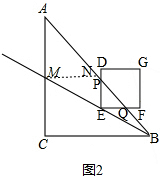 ,
,
∵MN∥BC,M为线段AC的中点,
∴N为线段AB的中点,
∴MN为△ABC的中位线,
∴MN=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∵DE∥AM,
∴△BPE∽△BAM,
∴$\frac{BE}{BM}=\frac{PE}{AM}$,
∴$\frac{\sqrt{5}t}{4\sqrt{5}}=\frac{PE}{4}$
解得PE=t.
∵EF∥MN,
∴△BEQ∽△BMN,
∴$\frac{BE}{BM}=\frac{EQ}{MN}$,
∴$\frac{\sqrt{5}t}{4\sqrt{5}}=\frac{EQ}{4}$,
解得EQ=t,
∴S=$\frac{1}{2}PE•EQ$=$\frac{1}{2}$t•t=$\frac{1}{2}$t2.
②当2<t≤4时,如图3,DG交AB于点P,FG交AB于点Q,延长EF交AB于点H,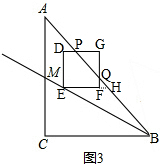 ,
,
由(2),可得EH=t,
∴FH=t-2,
∵∠QHF=∠ABC=45°,
∴QF=FH=t-2,
∴GQ=2-(t-2)=4-t,
∴PG=4-t,
∴S=2×2-$\frac{1}{2}$(4-t)2=-$\frac{1}{2}$t2+4t-4.
③当4<t≤5时,如图4,EF交AC于点H,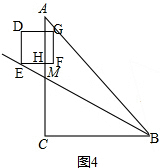 ,
,
∵EF∥BC,
∴$\frac{EH}{BC}=\frac{EM}{BM}$,
∴$\frac{EH}{8}=\frac{\sqrt{5}t-4\sqrt{5}}{4\sqrt{5}}$,
解得EH=2t-8,
∴HF=2-(2t-8)=10-2t,
∴S=GF•HF=2×(10-2t)=20-4t.
综上,可得
S=$\left\{\begin{array}{l}{{\frac{1}{2}t}^{2},0≤t≤2}\\{-{\frac{1}{2}t}^{2}+4t-4,2<t≤4}\\{20-4t,4<t≤5}\end{array}\right.$.
(3)①当旋转角为0°时,如图5,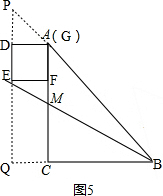 ,
,
点F在AC上,点P、Q分别在BA、BC的延长线上,
△BPQ是等腰直角三角形,
∴BP=BA+AP=$8\sqrt{2}+2\sqrt{2}=10\sqrt{2}$.
②当旋转角为45°时,如图6,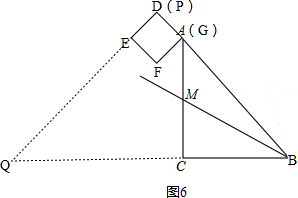 ,
,
点P与点D重合,△BPQ为等要直角三角形,
∴BP=BD=BA+AD=8$\sqrt{2}$+2.
③当旋转角为180°时,如图7,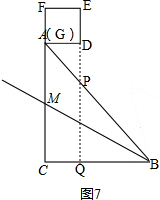 ,
,
点P在AB上,点Q在BC上,△BPQ为等要直角三角形,
∴BP=AB-AP=8$\sqrt{2}$-2$\sqrt{2}$=6$\sqrt{2}$.
④当旋转角为225°时,如图8,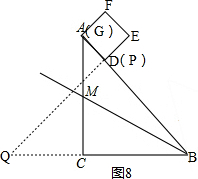 ,
,
点P、D重合在AB上,点Q在BC的延长线上,
△BPQ为等要直角三角形,
∴BP=BD=AB-AD=8$\sqrt{2}$-2.
点评 (1)此题主要考查了相似形综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.

| A. | $\sqrt{81}$=±9 | B. | (-$\frac{1}{3}$)2=$\frac{1}{9}$ | C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | |$\sqrt{3}$-2|=2-$\sqrt{3}$ |
| A. | (2a2)4=8a6 | B. | a3+a=a4 | C. | (a-b)2=a2-b2 | D. | a2÷a=a |
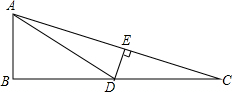 如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度.
如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°.若CD=1,求AB的长度. 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.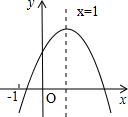 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2a+b=0;⑤a+b>m(am+b)(m≠1的实数).其中正确的结论有( )