��Ŀ����
7����ͼ����Rt��ABC�У���ACB=90�㣬AC=6cm��sinB=$\frac{3}{5}$����D��E��F�ֱ��DZ�AB��BC��AC���е㣬����DE��DF������P��Q�ֱ�ӵ�A��Bͬʱ�������˶��ٶȾ�Ϊ1cm/s����P��A��F��D�ķ����˶�����Dֹͣ����Q��BC�ķ����˶�������Pֹͣ�˶�ʱ����QҲֹͣ�˶������˶������У�����Q��BC�Ĵ��߽�AB�ڵ�M���Ե�P��M��QΪ������ƽ���ı���PMQN����ƽ���ı��α���PMQN�����FDEC�ص����ֵ����Ϊy��cm2������P�˶���ʱ��Ϊt��s������1������P�˶�����Fʱ��MQ=$\frac{9}{4}$cm��
��2���ڵ�P�ӵ�F�˶�����D�Ĺ����У�ijһʱ�̣���P����MQ�ϣ����ʱBQ�ij��ȣ�
��3���Ƿ����ijһʱ��t��ʹƽ���ı��α���PMQN�����FDEC�ص�������ƽ���ı��������Ϊ$\frac{15}{2}$�������ڣ����t��ֵ���������ڣ���˵�����ɣ�
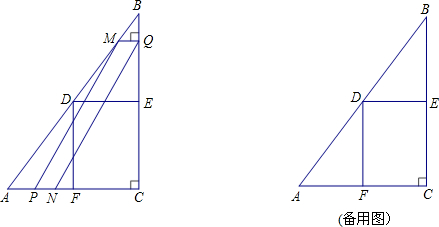
���� ��1������P�˶�����Fʱ�����AF=FC=3cm��BQ=AF=3cm����������𰸣�
��2�������ڵ�P�ӵ�F�˶�����D�Ĺ����У���P����MQ�ϵó�����t+t-3=8��������ɣ�
��3�����DE=$\frac{1}{2}$AC=3��DF=$\frac{1}{2}$BC=4��֤��MBQ�ס�ABC�����MQ=$\frac{3}{4}$t����Ϊ����������ٵ�3��t��4ʱ���ص�����ͼ��Ϊƽ���ı��Σ�����y=PN•PD����������ɣ��ڵ�4��t��$\frac{11}{2}$ʱ���ص�����Ϊ���Σ�����ͼ�εó�y=3[��8-t��-��t-3��]���۵�$\frac{11}{2}$��t��7ʱ���ص�����ͼ��Ϊ���Σ�����ͼ�εó�y=3[��t-3��-��8-t��]��������ɣ�
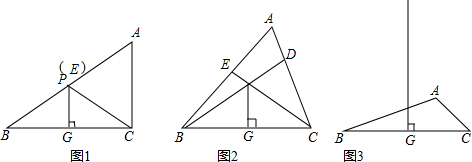
��� �⣺��1����ͼ1������Rt��ABC�У���ACB=90�㣬AC=6cm��sinB=$\frac{3}{5}$��
��$\frac{AC}{AB}$=$\frac{3}{5}$����$\frac{6}{AB}$=$\frac{3}{5}$��
��AB=10cm��
�ɹ��ɶ������BC=8cm��
����P�˶�����Fʱ��
��FΪAC���е㣬AC=6cm��
��AF=FC=3cm��
��P��Q���˶��ٶȶ���1cm/s��
��BQ=AF=3cm��
��MQ��AC��
��$\frac{MQ}{AC}$=$\frac{BQ}{BC}$����$\frac{MQ}{6}$=$\frac{3}{8}$��
���MQ=$\frac{9}{4}$��cm����
�ʴ�Ϊ��$\frac{9}{4}$��
��2�����ڵ�P�ӵ�F�˶�����D�Ĺ����У���P����MQ�ϣ���ͼ1��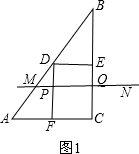
��t+t-3=8��
t=$\frac{11}{2}$��
BQ�ij���Ϊ$\frac{11}{2}$��1=$\frac{11}{2}$��cm����
��3����D��E��F�ֱ���AB��BC��AC���е㣬
��DE=$\frac{1}{2}$AC=$\frac{1}{2}$��6=3��
DF=$\frac{1}{2}$BC=$\frac{1}{2}$��8=4��
��MQ��BC��
���BQM=��C=90�㣬
�ߡ�QBM=��CBA��
���MBQ�ס�ABC��
��$\frac{BQ}{BC}$=$\frac{MQ}{AC}$��
��$\frac{t}{8}$=$\frac{MQ}{6}$��
MQ=$\frac{3}{4}$t��
��Ϊ����������ٵ�3��t��4ʱ���ص�����ͼ��Ϊƽ���ı��Σ���ͼ2��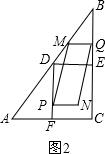 y=PN•PD
y=PN•PD
=$\frac{3}{4}$x��7-t��
��y=-$\frac{3}{4}$t2+$\frac{21}{4}$t��
��-$\frac{3}{4}$t2+$\frac{21}{4}$t=$\frac{15}{2}$��
�������t-2����t-5��=0��
���t1=2����ȥ����t2=5��
����t=5ʱ��ƽ���ı��α���PMQN�����FDEC�ص�������ƽ���ı��������Ϊ$\frac{15}{2}$��
�ڵ�4��t��$\frac{11}{2}$ʱ���ص�����Ϊ���Σ���ͼ3��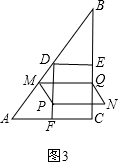 y=3[��8-t��-��t-3��]
y=3[��8-t��-��t-3��]
��y=-6t+33��
����-6t+33=$\frac{15}{2}$��
���t=$\frac{17}{4}$��
��t=$\frac{17}{4}$ʱ��ƽ���ı��α���PMQN�����FDEC�ص�������ƽ���ı��������Ϊ$\frac{15}{2}$��
�۵�$\frac{11}{2}$��t��7ʱ���ص�����ͼ��Ϊ���Σ���ͼ4��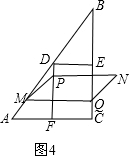 y=3[��t-3��-��8-t��]
y=3[��t-3��-��8-t��]
��y=6t-33��
��6t-33=$\frac{15}{2}$��
���t=$\frac{27}{4}$��
����t=$\frac{27}{4}$ʱ��ƽ���ı��α���PMQN�����FDEC�ص�������ƽ���ı��������Ϊ$\frac{15}{2}$��
������������t��ֵΪ5��$\frac{17}{4}$��$\frac{27}{4}$ʱ��ƽ���ı��α���PMQN�����FDEC�ص�������ƽ���ı��������Ϊ$\frac{15}{2}$��
���� ���⿼���˺�����Ӧ�ã����ε����ʣ�ƽ���ı��ε����ʣ������ε���λ�ߵ�֪ʶ���Ӧ�ã���Ҫ����ѧ���ۺ��������ʽ��м�������������˷�������˼�룮



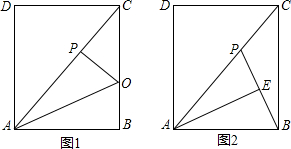
 ��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ���BC��AD�ڵ�E��F��
��ͼ����?ABCD�У�AB��AC��AB=1��BC=$\sqrt{5}$���Խ���AC��BD����O�㣬��ֱ��AC�Ƶ�O˳ʱ����ת���ֱ���BC��AD�ڵ�E��F��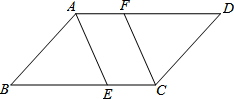 ��ͼ��ƽ���ı���ABCD�У���AB��AD����AE��CF�ֱ�ƽ�֡�BAD�͡�BCD
��ͼ��ƽ���ı���ABCD�У���AB��AD����AE��CF�ֱ�ƽ�֡�BAD�͡�BCD