题目内容
16.已知方程组$\left\{\begin{array}{l}{[x]+2y=1}\\{[y]+x=2}\end{array}\right.$其中[x],[y]分别表示不大于x,y的最大整数,则该方程组的解有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据题意结合[x],[y]分别表示不大于x,y的最大整数,得出x为整数以及2y一定是整数,进而分别分析得出答案.
解答 解:∵[y]+x=2,[y]表示不大于y的最大整数,
∴由结果为整数,可得x一定为整数,
∵[x]+2y=1,x为整数,
∴2y一定也是整数,当y=0,则x=1,此时[y]+x=2,中x=2,故此时不合题意,
即y≠0,
①当y是整数:原式可变为:$\left\{\begin{array}{l}{x+2y=1}\\{y+x=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$,
②当y不是整数,则y-0.5一定是整数,即[y]=y-0.5,
故原式可变为:$\left\{\begin{array}{l}{x+2y=1}\\{y-0.5+x=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=-1.5}\end{array}\right.$,
综上所述:该方程组的解有2组.
故选B.
点评 此题主要考查了取整计算以及二元一次方程组的解法,根据题意得出x,y的取值是解题关键.

练习册系列答案
相关题目
 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.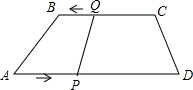 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.
如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.