题目内容
13.设O是等边三角形的中心,则向量$\overrightarrow{AB}$的长度是$\overrightarrow{OA}$长度的$\sqrt{3}$倍.分析 首先根据题意画出图形,然后由O是等边三角形的中心,利用三角函数的知识即可求得AB与AO的关系,继而求得答案.
解答 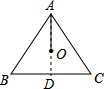 解:如图,延长AO交BC于点D,
解:如图,延长AO交BC于点D,
∵O是等边三角形的中心,
∴AD⊥BC,AD=$\frac{3}{2}$AO,∠B=60°,
∴AB=$\frac{AD}{sin60°}$=$\frac{2\sqrt{3}}{3}$AD,
∴AB=$\sqrt{3}$AO,
即向量$\overrightarrow{AB}$的长度是$\overrightarrow{OA}$长度的$\sqrt{3}$倍.
故答案为:$\sqrt{3}$.
点评 此题考查了平面向量的知识以及等边三角形的性质.注意根据题意画出图形,结合图形求解是关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
8. 如图,在△ABC中,AB=AC,AD=AE,BE=CD,则图中全等的三角形共有( )
如图,在△ABC中,AB=AC,AD=AE,BE=CD,则图中全等的三角形共有( )
 如图,在△ABC中,AB=AC,AD=AE,BE=CD,则图中全等的三角形共有( )
如图,在△ABC中,AB=AC,AD=AE,BE=CD,则图中全等的三角形共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |



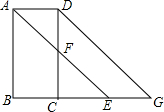 如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB
如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB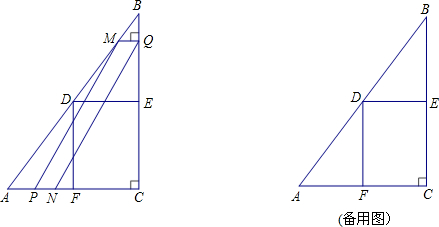
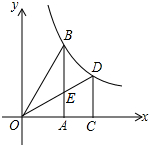 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.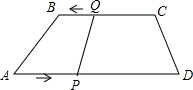 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.
如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.