题目内容
17.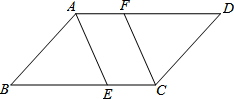 如图:平行四边形ABCD中,(AB≠AD),AE,CF分别平分∠BAD和∠BCD
如图:平行四边形ABCD中,(AB≠AD),AE,CF分别平分∠BAD和∠BCD①求证:AE=CF;
②若E是BC中点,求证:BC=2AB.
分析 ①根据平行四边形的性质可得AD∥BC,∠BAD=∠BCD,根据平行线的性质可得∠1+∠3=180°,∠2+∠4=180°,然后根据角平分线的性质可得∠1=∠2,进而可得∠3=∠4,然后可判定四边形AECF是平行四边形,从而得到AE=CF;
(2)根据角平分线和平行线的性质可证明∠5=∠6,从而可得AB=BE,再根据E是BC中点可证出结论.
解答 证明:①∵四边形ABCD是平行四边形,
∴AD∥BC,∠BAD=∠BCD,
∴∠1+∠3=180°,∠2+∠4=180°,
∵AE,CF分别平分∠BAD和∠BCD,
∴∠1=$\frac{1}{2}∠$BAD,∠2=$\frac{1}{2}∠$BCD,
∴∠1=∠2,
∴∠3=∠4,
∴四边形AECF是平行四边形,
∴AE=CF;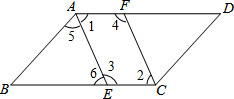
②∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠1=∠6,
∵AE平分∠BAD,
∴∠1=∠5,
∴∠5=∠6,
∴AB=BE,
∵E是BC中点,
∴BC=2BE,
∴BC=2AB.
点评 此题主要考查了平行四边形的判定和性质,关键是掌握平行四边形对边平行,对角线相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.一个角的度数是35°,那么这个角的余角是( )
| A. | 35° | B. | 45° | C. | 50° | D. | 55° |
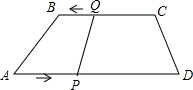 如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动.
如图所示,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,P,Q分别从点A,C同时出发,P以1厘米/秒的速度由A向D运动,Q以2厘米/秒的速度由C向B运动. 如图,在?ABCD中,已知AE⊥BC于点E,CF⊥AD于点F.请找出图中与BE相等的线段,并证明你的结论.
如图,在?ABCD中,已知AE⊥BC于点E,CF⊥AD于点F.请找出图中与BE相等的线段,并证明你的结论.
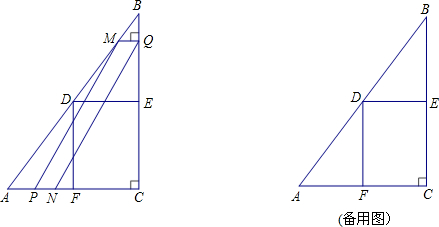
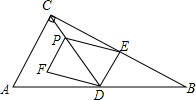 如图,在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作?EDFP,设点P的运动时间为t(秒).
如图,在△ABC中,∠ACB=90°,AC=2$\sqrt{5}$,BC=4$\sqrt{5}$,D、E分别是边AB、BC的中点,点P从点C出发,沿线段CD方向以每秒1个单位长度的速度运动,当点P与点D不重合时,以EP、ED为邻边作?EDFP,设点P的运动时间为t(秒).