题目内容
4. 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )| A. | (0,1) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
分析 △ABC绕点O顺时针旋转一周需6秒,而2017=6×336+1,所以第2017秒时,点A旋转到点A′,如图,则∠AOA′=60°,OA=OA′=1,作A′H⊥x轴于H,然后通过解直角三角形求出A′H和OH即可得到A′点的坐标.
解答 解: ∵360°÷60°=6,
∵360°÷60°=6,
2017=6×336+1,
∴第2017秒时,点A旋转到点A′,如图,
∠AOA′=60°,OA=OA′=1,
作A′H⊥x轴于H,
∵∠A′OH=30°,
∴A′H=$\frac{1}{2}$OA′=$\frac{1}{2}$,OH=$\sqrt{3}$A′H=$\frac{\sqrt{3}}{2}$,
∴A′($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$).
故选B.
点评 本题考查了坐标与图形变化-旋转:图形或点旋转之后要结合旋转的角度和图形的特殊性质来求出旋转后的点的坐标.常见的是旋转特殊角度如:30°,45°,60°,90°,180°.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
 如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15.
如图,两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=6,DH=2,平移距离CF为3,则BE=3,阴影部分面积为15. 在四边形OABC中,AB∥OC,∠OAB=90°,∠OCB=60°,AB=2,OA=2$\sqrt{3}$.
在四边形OABC中,AB∥OC,∠OAB=90°,∠OCB=60°,AB=2,OA=2$\sqrt{3}$. 如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图,在△ABC中,AB=AC=5,AB边上的高CD=4,点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动,当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).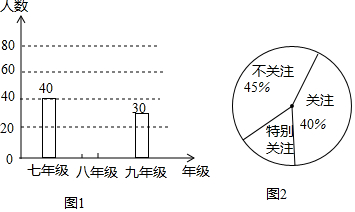
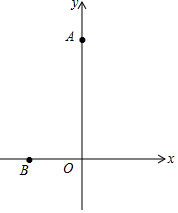 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.