题目内容
15．
如图，两个直角三角形重叠在一起，将其中一个三角形沿着点B到点C的方向平移到△DEF的位置，AB=6，DH=2，平移距离CF为3，则BE=3，阴影部分面积为15．
分析 先判断出阴影部分面积等于梯形ABEH的面积，再根据平移变化只改变图形的位置不改变图形的形状可得DE=AB，然后求出HE，根据平移的距离求出BE=CF=3，然后利用梯形的面积公式列式计算即可得解．
解答 解：∵△ABC沿着点B到点C的方向平移到△DEF的位置，
∴△ABC的面积=△DEF的面积，
∴阴影部分面积等于梯形ABEH的面积，
由平移的性质得，DE=AB=6，BE=CF=3，
∵AB=6，DH=2，
∴HE=DE-DH=6-2=4，
∴阴影部分的面积=$\frac{1}{2}$×（4+6）×3=15．
故答案为：3，15．
点评 本题考查了平移的性质，对应点连线的长度等于平移距离，平移变化只改变图形的位置不改变图形的形状，熟记各性质并判断出阴影部分面积等于梯形ABEH的面积是解题的关键．
练习册系列答案
相关题目
5．（1）如图1，AB=AD，∠B=∠D，∠1=∠2，求证：△ABC≌△ADE．
（2）如图2，已知，AD是△ABC的BC边上的中线，点E，F分别是AD及其延长线上的点，且DE=DF，求证：BF∥CE．
（2）如图2，已知，AD是△ABC的BC边上的中线，点E，F分别是AD及其延长线上的点，且DE=DF，求证：BF∥CE．
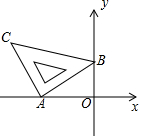含45°角的直角三角板如图放置在平面直角坐标系中，其中A（-2，0），B（0，1），则直线BC的解析式为y=-$\frac{1}{3}$x+1．
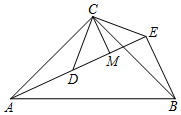如图，已知△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A、D、E在同一直线上，CM⊥AE于点M，连结BE．
4．
如图所示，平面直角坐标系的原点O是等边△ABC的中心，A（0，1），把△ABC绕点O顺时针旋转，每秒旋转60°，则第2017秒时，点A的坐标为（ ）
如图所示，平面直角坐标系的原点O是等边△ABC的中心，A（0，1），把△ABC绕点O顺时针旋转，每秒旋转60°，则第2017秒时，点A的坐标为（ ）| A． | （0，1） | B． | （$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） | C． | （$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$） | D． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$） |