��Ŀ����
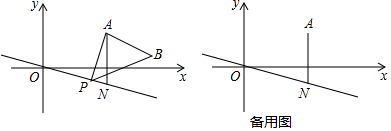
19�� ���ı���OABC�У�AB��OC����OAB=90�㣬��OCB=60�㣬AB=2��OA=2$\sqrt{3}$��
���ı���OABC�У�AB��OC����OAB=90�㣬��OCB=60�㣬AB=2��OA=2$\sqrt{3}$����1����ͼ1������OB����ֱ��д��OB�ij��ȣ�
��2����ͼ2������O��OH��BC�ڽ�BC��H������P�ӵ�H���������߶�HO���O�˶�������Q�ӵ�O���������߶�OA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ����P�˶���ʱ��Ϊt�룬��OPQ�����ΪS��ƽ����λ����
����S��t֮��ĺ�����ϵʽ��
����PQ��OB���ڵ�M������OPM�ȵ���������ʱ���������OPQ�����S��ֵ��
���� ��1�����ݹ��ɶ����������OB�ij���
��2���ٸ�������ó���BOCΪ�ȱ������Σ������ó�OH�ij����Ӷ���ʾ��OP�ij�����һ����ʾ��P�����꣬��������S=$\frac{1}{2}$OQ•xp������ɣ������ã�i����OM=PM����ii����OP=OM����iii����OP=PM���ֱ�����ó����ɣ�
��� �⣺��1������Rt��ABO�У�AB=2��OA=2$\sqrt{3}$��
��OB=$\sqrt{A{B}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+��2\sqrt{3}��^{2}}$=4��
��2������ͼ������ƽ������ϵ��
��tan��ABO=$\frac{AO}{AB}$=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$��
���ABO=60�㣬
��AB��OC��
���ABO=��BOC=60�㣬
�ߡ�BCO=60�㣬
���BOCΪ�ȱ������Σ�
��OH=OB•cos30��=4��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��
��OH=AO=2$\sqrt{3}$��
��OP=OH-PH=2$\sqrt{3}$-t��
��xp=OP•cos30��=3-$\frac{\sqrt{3}}{2}$t��yp=OP•sin30��=$\sqrt{3}$-$\frac{t}{2}$��
��S=$\frac{1}{2}$OQ•xp
=$\frac{1}{2}$t��3-$\frac{\sqrt{3}}{2}$t��
=-$\frac{\sqrt{3}}{4}$t2+$\frac{3}{2}$t ��0��t��2$\sqrt{3}$����
������OPM������������
��i����ͼ2����OM=PM����MPO=��MOP=��POC��
��PQ��OC��
��OQ=yp
��t=$\sqrt{3}$-$\frac{t}{2}$��
��ã�t=$\frac{2\sqrt{3}}{3}$��
��ʱS=-$\frac{\sqrt{3}}{4}$����$\frac{2\sqrt{3}}{3}$��2+$\frac{3}{2}$��$\frac{2\sqrt{3}}{3}$=$\frac{2\sqrt{3}}{3}$��
��ii����ͼ3����OP=OM����OPM=��OMP=75�㣬
���OQP=45�㣬
����P��PE��OA������ΪE�����У�EQ=EP��
��t-��$\sqrt{3}$-$\frac{1}{2}$t��=3-$\frac{\sqrt{3}}{2}$t��
��ã�t=2��
��ʱS=-$\frac{\sqrt{3}}{4}$��22+$\frac{3}{2}$��2=3-$\sqrt{3}$��
��iii����OP=PM����POM=��PMO=��AOB��
��PQ��OA��
��ʱQ��AB�ϣ����������⣮
���� ������Ҫ�������ı����ۺ��Լ�������Ǻ�����ϵ�͵ȱ������Ρ����������ε����ʵ�֪ʶ�����÷������۵ó��ǽ���ؼ���

 ��һ������ĩ�ٷֳ�̾�ϵ�д�
��һ������ĩ�ٷֳ�̾�ϵ�д� ��ͼ��ʾ��ƽ��ֱ������ϵ��ԭ��O�ǵȱߡ�ABC�����ģ�A��0��1�����ѡ�ABC�Ƶ�O˳ʱ����ת��ÿ����ת60�㣬���2017��ʱ����A������Ϊ��������
��ͼ��ʾ��ƽ��ֱ������ϵ��ԭ��O�ǵȱߡ�ABC�����ģ�A��0��1�����ѡ�ABC�Ƶ�O˳ʱ����ת��ÿ����ת60�㣬���2017��ʱ����A������Ϊ��������| A�� | ��0��1�� | B�� | ��$\frac{\sqrt{3}}{2}$��$\frac{1}{2}$�� | C�� | ��$\frac{\sqrt{3}}{2}$��-$\frac{1}{2}$�� | D�� | ��-$\frac{\sqrt{3}}{2}$��-$\frac{1}{2}$�� |
 ��ͼ��������ABCD�У�DE��AB��cosA=$\frac{3}{5}$��BE=3����tan��DBE��ֵ�ǣ�������
��ͼ��������ABCD�У�DE��AB��cosA=$\frac{3}{5}$��BE=3����tan��DBE��ֵ�ǣ�������| A�� | $\frac{4}{3}$ | B�� | 2 | C�� | $\frac{\sqrt{5}}{2}$ | D�� | $\frac{\sqrt{5}}{5}$ |
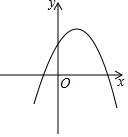 ���κ���y=ax2-3ax+2��a��0����ͼ����ͼ��ʾ����y��2����x��ȡֵ��ΧΪx��0��x��3��
���κ���y=ax2-3ax+2��a��0����ͼ����ͼ��ʾ����y��2����x��ȡֵ��ΧΪx��0��x��3��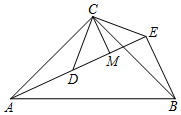 ��ͼ����֪��ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CM��AE�ڵ�M������BE��
��ͼ����֪��ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90�㣬��A��D��E��ͬһֱ���ϣ�CM��AE�ڵ�M������BE��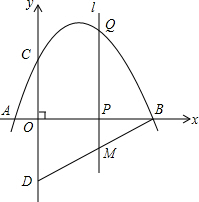 ��ͼ��������y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 �� x �ύ�ڵ� A���� B���� y �ύ�ڵ�C����D ���C���� x ��Գƣ��� P �� x ���ϵ�һ�����㣬���P ������Ϊ��m��0�������� P �� x ��Ĵ��� l ���������ڵ� Q��
��ͼ��������y=-$\frac{1}{2}$x2+$\frac{5}{2}$x+3 �� x �ύ�ڵ� A���� B���� y �ύ�ڵ�C����D ���C���� x ��Գƣ��� P �� x ���ϵ�һ�����㣬���P ������Ϊ��m��0�������� P �� x ��Ĵ��� l ���������ڵ� Q��