题目内容
16.2017年3月23日,在世界杯预赛亚洲区12强赛A组6轮的较量中,中国足球队以1-0的比分战胜老对手韩国队晋级12强.某初中学校为了了解本校800名学生对本次比赛的关注程度,以便做好引导和教育工作,随机抽取了150名学生进行调查,按年级人数和关注程度,分别绘制了条形统计图(图1)和扇形统计图(图2).(1)请你补全条形统计图,并求“特别关注”所在扇形的圆心角的度数;
(2)求全校不关注本场比赛的学生大约有多少名?
(3)在这次调查中,九年级共有两位男生和两位女生“不关注”本次比赛,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是一男生和一女生的概率.
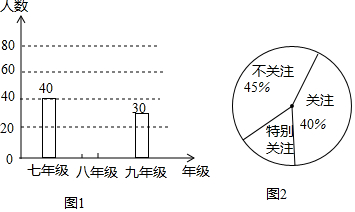
分析 (1)用抽取的总人数减去七、九年级人数可得,再用360度乘以“特别关注”的百分比;
(2)全校人数乘以样本中不关注比赛的百分比可得;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到一男生和一女生的情况,再利用概率公式即可求得答案.
解答 解:(1)根据题意可得,八年级人数为150-(40+30)=80(人),
“特别关注”所在扇形的圆心角的度数为360°×(1-45%-40%)=54°,补全条形统计图如下:
(2)800×45%=360,
答:全校不关注本场比赛的学生大约有360名;
(3)画树状图得:
∵共有12种等可能的结果,抽取的两人恰好是一男生和一女生的有8种结果,
∴抽取的两人恰好是一男生和一女生的概率为$\frac{8}{12}$=$\frac{2}{3}$.
点评 此题考查了树状图法与列表法求概率以及频率分布直方图.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4. 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )| A. | (0,1) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
8. 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
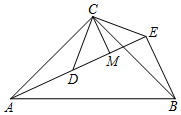 如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.
如图,已知△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM⊥AE于点M,连结BE.
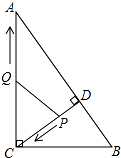 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.