题目内容
13.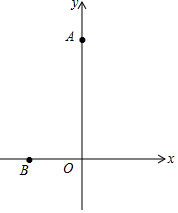 如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
如图,在平面直角坐标系中,已知A(0,4),B(-1,0),在y轴上有一动点G,则BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
分析 在x轴上取一点E($\sqrt{2}$,0),则AE=$\sqrt{O{A}^{2}+O{E}^{2}}$=3$\sqrt{2}$.作GF⊥AE于F,GH⊥AE于H,交OA于G′,由△AFG∽△AOB,可得$\frac{GF}{OE}$=$\frac{AG}{AE}$,推出GF=$\frac{1}{3}$AG,推出BG+$\frac{1}{3}$AG=BG+FG,
根据垂线段最短可知,当G与G′重合时,BG+$\frac{1}{3}$AG的值最小,最小值为BH,求出BH即可解决问题.
解答 解:在x轴上取一点E($\sqrt{2}$,0),则AE=$\sqrt{O{A}^{2}+O{E}^{2}}$=3$\sqrt{2}$.
作GF⊥AE于F,GH⊥AE于H,交OA于G′
∵∠GAF=∠OAE,∠AFG=∠AOE,
∴△AFG∽△AOB,
∴$\frac{GF}{OE}$=$\frac{AG}{AE}$,
∴$\frac{GF}{\sqrt{2}}$=$\frac{AG}{3\sqrt{2}}$,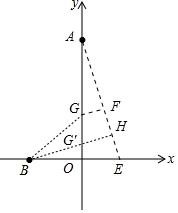
∴GF=$\frac{1}{3}$AG,
∴BG+$\frac{1}{3}$AG=BG+FG,
根据垂线段最短可知,当G与G′重合时,BG+$\frac{1}{3}$AG的值最小,最小值为BH,
∵∠BEH=∠AEO,∠BHE=∠AOE,
∴△BHE∽△AOE,
∴$\frac{BH}{AO}$=$\frac{BE}{AE}$,
∴$\frac{BH}{4}$=$\frac{1+\sqrt{2}}{3\sqrt{2}}$,
∴BH=$\frac{4+2\sqrt{2}}{3}$,
∴BG+$\frac{1}{3}$AG的最小值为$\frac{4+2\sqrt{2}}{3}$.
故答案为$\frac{4+2\sqrt{2}}{3}$.
点评 本题考查垂线段最短、勾股定理、相似三角形的判定和性质等知识,解题的关键是添加辅助线,关注相似三角形解决问题,属于中考填空题中的压轴题.

 如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )
如图所示,平面直角坐标系的原点O是等边△ABC的中心,A(0,1),把△ABC绕点O顺时针旋转,每秒旋转60°,则第2017秒时,点A的坐标为( )| A. | (0,1) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | C. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) |
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=3,则tan∠DBE的值是( )| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | 在足球赛中,弱队战胜强队 | |
| B. | 长分别为3、5、9厘米的三条线段能围成一个三角形 | |
| C. | 抛掷一枚硬币,落地后正面朝上 | |
| D. | 任取两个正整数,其和大于1 |
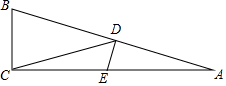 如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E.
如图,在△ABC中,∠ACB=90°,∠A=15°,D是边AB的中点,DE⊥AB交AC于点E. 在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.
在矩形ABCD中,AB=6,AD=8,P是BC边上一个动点(不与点B重合).设PA=x,点D到PA的距离为y,求y与x之间的函数表达式,并求出自变量x的取值范围.